СЛУЧАЙНОЙ СОСТАВЛЯЮЩЕЙ
1. ЦЕЛЬ РАБОТЫ
Цель работы заключается в освоении инструментария системы Gretl в области построения и анализа регрессионных моделей с гетероскедастичной случайной составляющей для выявления и последующего применения ранее неизвестных закономерностей в имеющихся данных в процессе подготовки и принятия решений менеджерами компаний.
2. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Для регрессионной модели, формула (1), построенной по фактическим данным типа срез данных (cross-sectional) дисперсия случайных отклонений (ошибок) часто представляет собой переменную величину
где y — фактическое значение результативного признака;
ai – параметр регрессионной модели;
Данная ситуация представляет собой проблему гетероскедастичности («неодинакового разброса») - нарушения, возникающего при невыполнении одного из классических предположений линейного регрессионного анализа о постоянстве дисперсий случайных отклонений (гомоскедастичности или «одинакового разброса» - математическое ожидание случайной составляющей, М(ui) =0 - отсутствие автокорреляции остатков (взаимосвязи ui и ui-1). - случайный характер остатков – их независимость от yi и xi. Случаи гетероскедастичности и гомоскедастичности показаны на рисунках 1 и 2 соответственно.
Гетероскедастичность приводит к тому, что при применении обычного метода наименьших квадратов (1МНК) полученные параметры Наблюдение, для которого теоретическое распределение ошибки имеет малое стандартное отклонение, будет обычно находится близко к линии регрессии и, следовательно, может стать хорошим ориентиром, указывающим на место этой линии. В противоположность этому наблюдение, где теоретическое распределение имеет большое стандартное отклонение, не сможет в той же мере помочь в определении местоположения линии регрессии. Обычный МНК не делает различия между качеством наблюдений, придавая одинаковые "веса" каждому из них независимо от того, является ли наблюдение существенным или несущественным для определения местоположения этой линии. Следовательно, обычным МНК мы получим неэффективные оценки коэффициентов. Также результаты t- и F- тестов будут ненадёжными, т.к. мы получим неверные оценки стандартных ошибок параметров Поскольку в данном случае использование обычного метода наименьших квадратов (1МНК) неэффективно, необходимо сделать поправку на гетероскедастичность, применив взвешенный метод наименьших квадратов ВМНК (WLS) для её устранения.
Построение гетероскедастичной регрессионной модели состоит из двух этапов: 1. Обнаружение гетероскедастичности случайной составляющей, 2. Оценивание модели с использованием взвешенного метода наименьших квадратов (WLS). На первом этапе в случае однофакторной регрессии Затем проводится один из формальных тестов на гетероскедастичность: тест ранговой корреляции Спирмена, тест Парка (The Park test), тест Голдфелда-Квандта (Goldfeld-Quandt test), тест Бреуша-Погана, тест Глейзера, или тест Уайта (White’s test) и осуществляется интерпретация результатов теста. В каждом тесте пытаются опровергнуть гипотезу о гомоскедастичности, если это удаётся, то можно сделать вывод, что в модели наблюдается гетероскедастичность. Рассмотрим алгоритм теста Уайта на гетероскедастичность, не требующего нормальности распределения остатков. Алгоритм состоит из следующих шагов: - Получение остатков оцененной регрессионной модели - Оценивание вспомогательного уравнения регрессии квадратов остатков относительно комплекса переменных модели, их произведений и их квадратов - Проверка общей значимости уравнения с помощью критерия На втором этапе для оценки моделей с гетероскедастичностью используется взвешенный метод наименьших квадратов (ВМНК - WLS). Метод ВМНК, как и 1МНК, применим к однофакторной и множественной линейной регрессии и использует то же правило минимизации суммы квадратов остатков, RSS, но вместо одинаковых весов для каждого наблюдения им приписываются значения, обратные соответствующим дисперсиям ошибки, что отражено формулой (2).
где
Тогда коэффициенты линейной регрессии находятся по формуле (3).
где W=diag{w1,…,wn} - диагональная матрица весов; n- число наблюдений. Дисперсия ошибки
|

 .
. , (1)
, (1) - модельное значение результативного признака;
- модельное значение результативного признака;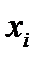 - признак-фактор;
- признак-фактор; — случайная ошибка.
— случайная ошибка. ), при этом остальные условия Гаусса-Маркова выполняются:
), при этом остальные условия Гаусса-Маркова выполняются:


 модели, формула (1), больше не представляют собой наиболее эффективные оценки или не являются оценками с минимальной дисперсией.
модели, формула (1), больше не представляют собой наиболее эффективные оценки или не являются оценками с минимальной дисперсией. (STDERROR), т.к. они вычисляются на основе предположения о том, что остатки модели гомоскедастичны, что скажется на правильности расчёта t- и F- статистик и приведёт к принятию ошибочных гипотез.
(STDERROR), т.к. они вычисляются на основе предположения о том, что остатки модели гомоскедастичны, что скажется на правильности расчёта t- и F- статистик и приведёт к принятию ошибочных гипотез. изначально проводится графический анализ остатков – строится и анализируется зависимость квадратов ошибок от
изначально проводится графический анализ остатков – строится и анализируется зависимость квадратов ошибок от  , или строится
, или строится  диаграмма рассеяния. При множественной регрессии графический анализ также возможен для каждой из объясняющих переменных. Рост дисперсии с ростом одного из факторов свидетельствует о гетероскедастичности.
диаграмма рассеяния. При множественной регрессии графический анализ также возможен для каждой из объясняющих переменных. Рост дисперсии с ростом одного из факторов свидетельствует о гетероскедастичности.

 . Тестовой статистикой является величина
. Тестовой статистикой является величина  (
( - число наблюдений,
- число наблюдений,  - коэффициент детерминации). Число степеней свободы равно числу регрессоров вспомогательного уравнения. Если
- коэффициент детерминации). Число степеней свободы равно числу регрессоров вспомогательного уравнения. Если 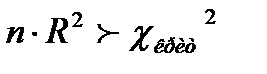 , то нулевая гипотеза гомоскедастичности Ho:
, то нулевая гипотеза гомоскедастичности Ho:  отвергается.
отвергается. , (2)
, (2) - фактическое и модельное i-е значение зависимой переменной;
- фактическое и модельное i-е значение зависимой переменной; – вес i-го наблюдения,
– вес i-го наблюдения,  ;
;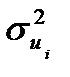 - дисперсия i-й случайной составляющей.
- дисперсия i-й случайной составляющей. , (3)
, (3) , например,
, например,  , где с- ненулевая константа и x1i - значение объясняющей переменной х1 в i-ом наблюдении. В случае подобного соотношения
, где с- ненулевая константа и x1i - значение объясняющей переменной х1 в i-ом наблюдении. В случае подобного соотношения  можно считать известными, т.к. постоянная величина «c» не влияет на взвешенную процедуру. Тогда значения весов
можно считать известными, т.к. постоянная величина «c» не влияет на взвешенную процедуру. Тогда значения весов  .
.


