Откроем встроенный набор данных attend.gdt на закладке Wooldridge (File\Open Data\Sample File\attend.gdt) и обратимся к функции Model\Ordinary Least Squares, чтобы построить линейную регрессионную модель, отражающую зависимость переменной Final (оценка за итоговый экзамен) от переменных attend (число посещённых занятий), termGPA (средний балл за семестр), priGPA (средний балл на начало семестра)енка за итоговый экзаменпритавлены на рис 5.симость...вызывается функцией меню вадратов, в частности, 1МНК (), ACT (оценка по вступительному тесту ACT), hwrte (процент сданных домашних В открывшемся окне спецификации модели выберем соответствующие зависимую и независимые переменные при помощи кнопок «Choose» и “Add”, затем нажмём кнопку ОК (рисунок 1).
Рисунок 1 - Окно спецификации эконометрической модели, оцениваемой с применением 1МНК
Полученные результаты представлены на рисунке 2. По данным наблюдений attend.gdt была составлена модель (9).
. (9)
Рассматривая значения параметров модели 
для данной отдельной выборки, можно отметить существенность зависимости переменной final от переменных termgpa (сильная положительная связь, 3,54) и ACT (положительная связь 0,272), остальные коэффициенты имеют значения близкие к 0 и не оказывают существенного влияния на результирующий признак. Необходимо установить насколько вероятно, что зависимость, подобная найденной, подтвердится на данных другой выборки, извлеченной из той же самой генеральной совокупности, т.е. можно ли свойства данной выборки перенести на всю генеральную совокупность.
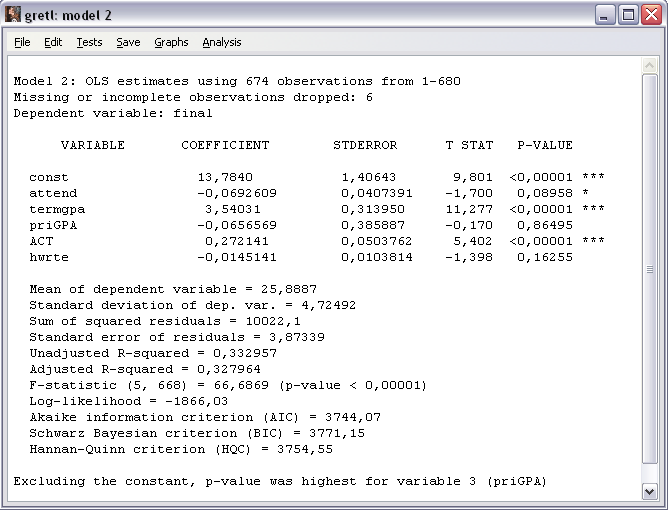
Рисунок 2 - Окно результатов моделирования с применением 1МНК
Рассмотрим сущность показателей (таблица 1), используемых в таблице регрессии окна результатов моделирования (рисунок 2):
Таблица 1- Показатели таблицы регрессии
| Variable -
| независимая переменная, существенность влияния которой необходимо оценить.
|
| Coefficient-
| коэффициент (параметр) модели,  , значимость которого необходимо оценить.
|
| Std. Error-
| стандартная ошибка параметра модели, является оценкой среднеквадратичного отклонения параметра регрессии от его истинного значения, даёт общую оценку степени точности параметра.
|
| T-STATISTIC-
| расчётные значения t- критерия Стьюдента, отношение значения параметра к STD.ERROR, формула (5).
|
| P-value-
| показывает вероятность того, что соответствующее значение критерия для генеральной совокупности может оказаться больше, чем расчётное значение по рассматриваемой выборке. Если p-value не превышает уровень значимости, то коэффициент является значимым и принимается альтернативная гипотеза.
|
| Mean of dependent variable-
| cреднее значение зависимой переменной (y).
|
| Standard deviation of dep. var.-
| стандартное (среднеквадратическое) отклонение зависимой переменной (y) – корень квадратный из дисперсии, мера разброса данных.
|
| Sum of squared residuals -
| сумма квадратов остатков (RSS=  ), измеряет необъяснённую часть вариации зависимой переменной, используется как основная минимизируемая величина в 1МНК.
|
| Standard error of residuals-
| стандартная ошибка регрессии (среднеквадратическое отклонение ошибки), оценивает степень соответствия модели эмпирическим данным и качество оценивания; измеряет величину квадрата ошибки, приходящейся на одну степень свободы модели (RSS2\(n-k))1\2.
|
| Unadjusted R2-
| нескорректированный коэффициент детерминации  - показывает долю объяснённой (уравнением регрессии) дисперсии зависимой переменной y, формула (7).
|
| Adjusted R2 -
| скорректированный коэффициент детерминации, используемый при необходимости учёта количества наблюдений и оцениваемых параметров, чтобы обеспечить сопоставимость различных моделей.
|
| F-statistic-
| расчетное значение F-критерия Фишера, формула (6), отношение объяснённой суммы квадратов (в расчёте на одну независимую переменную) к остаточной сумме квадратов (в расчёте не одну степень свободы)
|
| Log-likelihood -
| логарифмическая функция правдоподобия. Функция правдоподобия – это плотность распределения y.
|
| Akaike information criterion-
| информационный критерий Акайке, анализирует правильность спецификации модели. Позволяет выбирать наилучшую модель из множества различных спецификаций.
|
| Schwarz Bayesian criterion-
| информационный Байесовский критерий Шварца, анализирует правильность спецификации модели, позволяет выбирать наилучшую модель из множества различных спецификаций.
|
| Hannan-Quinn criterion-
| информационный критерий Хеннана – Куинна, анализирует правильность спецификации модели
|
| OLS
| 1МНК
|
| Model 2: estimates using 674 observations from 1-680
| модель2: использует для оценки 674 наблюдения из 680
|
| Missing or incomplete observations dropped
| число пропущенных наблюдений
|
| Dependent variable
| зависимая переменная (y)
|
