ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ О ЛИНЕЙНОМ РЕГРЕССИОННОМ АНАЛИЗЕ
Целью регрессионного анализа является оценка функциональной зависимости
где y — фактическое значение результативного признака;
ai – параметр регрессионной модели;
Оценивание параметров линейной модели основан на обычном или одношаговом методе наименьших квадратов (1МНК или OLS – Ordinary Least Squares). Этот метод позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака (y) от расчетных (теоретических)
Статистическое моделирование связи методом линейного регрессионного анализа осуществляется в 3 этапа: A) Оценка параметров линейной регрессионной модели методом 1МНК Вектор оценок параметров модели (2) определяется выражением (4). B) Проверка адекватности регрессионной модели (проверки значимости индивидуальных оценок коэффициентов модели с помощью t- критерия Стьюдента и оценка значимости уравнения регрессии в целом с помощью F-критерия Фишера) На первом шаге проверки адекватности (качества) модели оценивается существенность влияния каждой объясняющей переменной
где
На втором шаге проверки адекватности модели оценивается её значимость (пригодность) в целом, используя показатели: F-критерий Фишера, формула (6), коэффициент детерминации Значимость регрессии проверяется путём проверки нулевой гипотезы о равенстве нулю всех параметров модели (для выбранного уровня значимости).
где
k – число коэффициентов факторов. При анализе адекватности уравнения регрессии исследуемому процессу возможны следующие варианты: - Построенная модель на основе ее проверки по F-критерию Фишера в целом адекватна, и все коэффициенты регрессии значимы. Такая модель может быть использована для принятия решений к осуществлению прогнозов. - Модель по F-критерию Фишера адекватна, но часть коэффициентов регрессии незначима. В этом случае модель пригодна для принятия некоторых решений, но не для производства прогнозов.
- Модель по F-критерию Фишера адекватна, но все коэффициенты регрессии незначимы. Поэтому модель полностью считается неадекватной. На ее основе не принимаются решения и не осуществляются прогнозы.
|

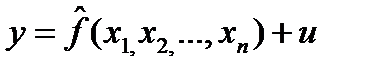 результативного признака (y) от факторных
результативного признака (y) от факторных 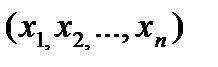 . Формулы (1) и (2) представляют собой линейные модели парной и множественной регрессии соответственно.
. Формулы (1) и (2) представляют собой линейные модели парной и множественной регрессии соответственно. , (1)
, (1) , (2)
, (2)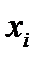 - признак-фактор;
- признак-фактор; — случайная ошибка (остаток), характеризующая отклонения реального значения результативного признака от теоретического. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.
— случайная ошибка (остаток), характеризующая отклонения реального значения результативного признака от теоретического. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.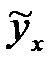 минимальна, формула (3).
минимальна, формула (3). , (3)
, (3)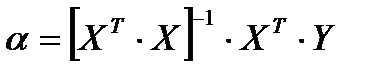 (4)
(4) , используя t- критерий Стьюдента, формула (5). Значимость параметра определяется путём проверки нулевой гипотезы о равенстве его нулю (для выбранного уровня значимости).
, используя t- критерий Стьюдента, формула (5). Значимость параметра определяется путём проверки нулевой гипотезы о равенстве его нулю (для выбранного уровня значимости). ,(5)
,(5) - оценка
- оценка 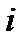 -го коэффициента модели, COEFFICIENT;
-го коэффициента модели, COEFFICIENT;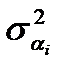 - оценка дисперсии параметра
- оценка дисперсии параметра 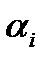 ,
,  = STDERROR.
= STDERROR. , формула (7), (Unadjusted R2 и Adjusted R2), сумма квадратов остатков RSS Sum of squared residuals), стандартная ошибка регрессии (Standard error of residuals), информационные критерии (Akaike information criterion, Schwarz Bayesian criterion, Hannan-Quinn criterion).
, формула (7), (Unadjusted R2 и Adjusted R2), сумма квадратов остатков RSS Sum of squared residuals), стандартная ошибка регрессии (Standard error of residuals), информационные критерии (Akaike information criterion, Schwarz Bayesian criterion, Hannan-Quinn criterion).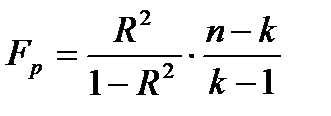 , (6)
, (6)
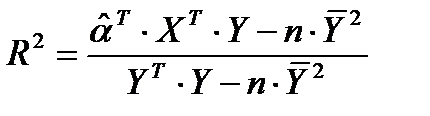 , (7)
, (7)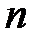 - число наблюдений;
- число наблюдений;


