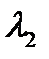Метод главных компонент был предложен Пирсоном в 1901 году и затем вновь открыт и детально разработан Хоттелингом (1933г.) Данный метод применяется, например, для сжатия объемов хранимой информации и упрощения её интерпретации или сравнения многомерных исследуемых объектов, позволяя снизить размерность исходного признакового пространства 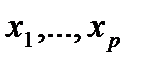 (
( - исходный признак) и перейти к новым агрегированным признакам
- исходный признак) и перейти к новым агрегированным признакам 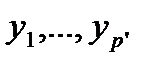 (
(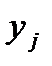 -главная компонента),
-главная компонента), 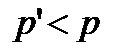 . При этом новые показатели
. При этом новые показатели 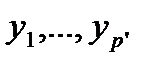 представляют собой линейные комбинации исходных
представляют собой линейные комбинации исходных 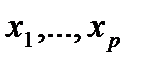 , коррелированных между собой, формула (1).
, коррелированных между собой, формула (1).
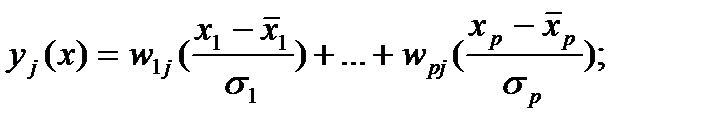

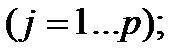 (1)
(1)

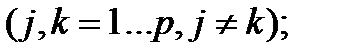
где 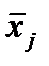 и
и  — среднее арифметическое и среднеквадратическое отклонение признака xi.;
— среднее арифметическое и среднеквадратическое отклонение признака xi.;
wij - коэффициенты главных компонент, максимизирующие дисперсию yj, которые находятся из уравнения  , имеющее решение, если
, имеющее решение, если 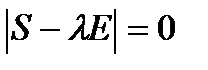 , где S- ковариационная (или корреляционная) матрица;
, где S- ковариационная (или корреляционная) матрица;
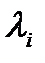 - собственные числа матрицы S - равны дисперсиям проекций множества объектов на оси главных компонент (или диагоналям эллипса рассеяния), рисунок 1. На рисунке 1 “p” точек сосредоточены в трехмерном пространстве двух систем координат: переменных x1, x2, x3 и главных компонент у1, у2, у3. При этом оси ОУ1, ОУ2, ОУ3 проходят через центр тяжести эллипсоида рассеяния.
- собственные числа матрицы S - равны дисперсиям проекций множества объектов на оси главных компонент (или диагоналям эллипса рассеяния), рисунок 1. На рисунке 1 “p” точек сосредоточены в трехмерном пространстве двух систем координат: переменных x1, x2, x3 и главных компонент у1, у2, у3. При этом оси ОУ1, ОУ2, ОУ3 проходят через центр тяжести эллипсоида рассеяния.
Традиционный алгоритм расчета главных компонент включает переход от исходной матрицы наблюдений Х к ковариационной (или корреляционной) матрице S между исходными признаками 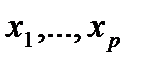 , далее к расчету собственных чисел
, далее к расчету собственных чисел 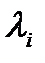 . Основываясь на наибольших собственных числах, наилучшим образом объясняющих исходное пространство признаков, производится переход к главным компонентам путём определения их коэффициентов wj= (w1j,...,wpj) ', максимизирующих дисперсию проекций множества объектов на оси главных компонент. Таким образом, выбираются только те главные компоненты, изменчивость которых покрывает большую часть изменчивости
. Основываясь на наибольших собственных числах, наилучшим образом объясняющих исходное пространство признаков, производится переход к главным компонентам путём определения их коэффициентов wj= (w1j,...,wpj) ', максимизирующих дисперсию проекций множества объектов на оси главных компонент. Таким образом, выбираются только те главные компоненты, изменчивость которых покрывает большую часть изменчивости 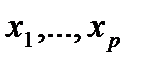 .
.

Рисунок 1 – Диаграмма рассеяния x1, x2, x3


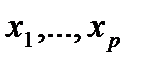 (
( - исходный признак) и перейти к новым агрегированным признакам
- исходный признак) и перейти к новым агрегированным признакам 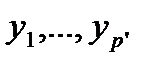 (
(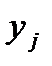 -главная компонента),
-главная компонента), 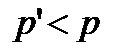 . При этом новые показатели
. При этом новые показатели 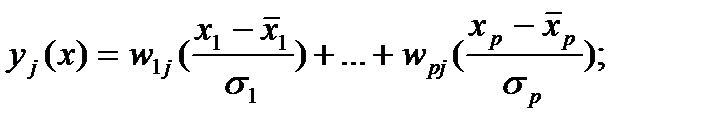

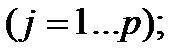 (1)
(1)
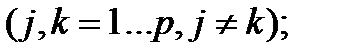
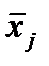 и
и  — среднее арифметическое и среднеквадратическое отклонение признака xi.;
— среднее арифметическое и среднеквадратическое отклонение признака xi.; , имеющее решение, если
, имеющее решение, если 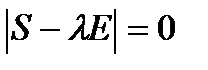 , где S- ковариационная (или корреляционная) матрица;
, где S- ковариационная (или корреляционная) матрица;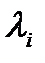 - собственные числа матрицы S - равны дисперсиям проекций множества объектов на оси главных компонент (или диагоналям эллипса рассеяния), рисунок 1. На рисунке 1 “p” точек сосредоточены в трехмерном пространстве двух систем координат: переменных x1, x2, x3 и главных компонент у1, у2, у3. При этом оси ОУ1, ОУ2, ОУ3 проходят через центр тяжести эллипсоида рассеяния.
- собственные числа матрицы S - равны дисперсиям проекций множества объектов на оси главных компонент (или диагоналям эллипса рассеяния), рисунок 1. На рисунке 1 “p” точек сосредоточены в трехмерном пространстве двух систем координат: переменных x1, x2, x3 и главных компонент у1, у2, у3. При этом оси ОУ1, ОУ2, ОУ3 проходят через центр тяжести эллипсоида рассеяния.