Пример построения полиномиальной модели тренда
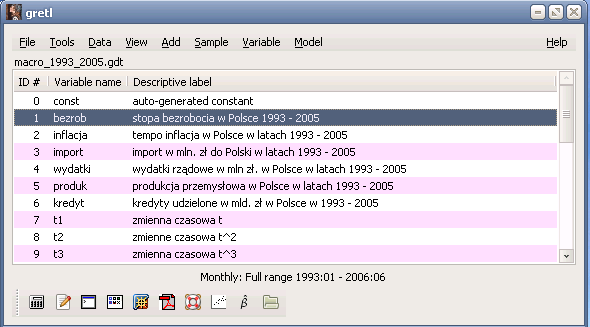
Для построения модели полиномиального тренда в Gretl 1.7.1 из меню Model выбирается пункт Ordinary Least Squares (рисунок 2). Продемонстрируем выбор степени полинома относительно переменной времени t при построении модели тренда на примере ежемесячных данных об уровне безработицы в Польше с 1993 по 2005 год (файл macro_1993_2005 доступен на сайте www.kufel.torun.pl/ru). Откроем набор исходных данных macro_1993_2005 на закладке KUFEL, выбрав пункт меню File\Open Data\Sample file или создадим его, перенеся данные Приложения А в файл macro.xls и импортировав его в пакет Gretl. Для этого в меню Gretl выберем команду File\Open Data\Import\Excel, в появившемся окне укажем номер строки и столбца начала таблицы Excel и нажмём кнопку ОК, в следующем окне нажмём кнопку YES, затем выберем тип данных временной ряд (time series), нажмём кнопку FORWARD, отметим периодичность данных MONTHLY, нажмём кнопку FORWARD, введём год и месяц начала сбора данных 1993:01, нажмём кнопку FORWARD и ОК. Сохраним созданный набор данных (рисунок 2) File\Save Data как файл macro_1993_2005 на рабочем столе.
Рисунок 2 – Набор данных macro_1993_2005
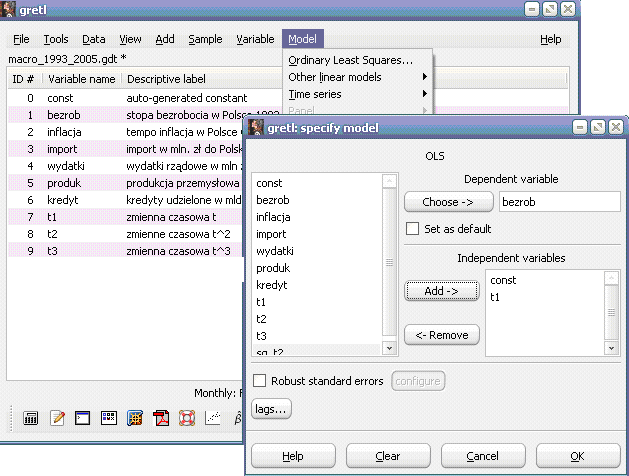
Обратимся к команде Model\Ordinary Least Squares (метод наименьших квадратов). Для построения модели линейного тренда в открывшемся окне спецификации модели (рисунок 3) при помощи кнопки Choose выберем зависимую переменную Y (Dependent variable) – уровень безработицы (bezrob) и добавим объясняющую переменную X при помощи кнопки ADD (переменная времени t1 указывает номер месяца), нажмём кнопку ОК.
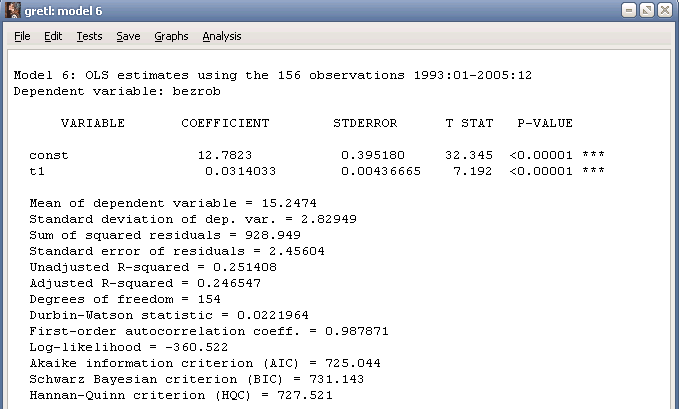
Рисунок 3 – Построение модели линейного тренда Результаты оценивания линейного тренда показаны в окне результатов моделирования (рисунок 4) и на графике (рисунок 5). Полученная модель Из визуального анализа графика (рисунок 5) можно сделать вывод, что исходные данные представляют собой нестационарный временной ряд с выраженной цикличностью данных: ряд имеет тенденцию (непостоянное среднее), непостоянную дисперсию, существенные периодические колебания. еменном значении дисперсии ()ым
Рисунок 4 – Окно результатов моделирования линейного тренда ряда bezrob Рисунок 5 – Фактические данные и график линейного тренда Для прогнозирования будущих значений временного ряда bezrob необходимо добавить соответствующее число «пустых» наблюдений к набору данных, например, 6 для составления прогноза на январь-июнь 2006 года. Для этого обратимся к команде Data\Add observations…, введём число добавляемых наблюдений в открывшемся окне (6) и нажмём кнопку ОК (рисунок 6).
Рисунок 6 – Добавление «пустых» наблюдений к переменным набора данных macro_1993_2005 Затем повторим описанную выше последовательность действий по построению модели линейного тренда. В окне результатов моделирования (рисунок 4) выберем пункт Forecasts меню Analysis. В открывшемся окне введём общее число наблюдений до составления прогноза 156 и период для составления прогноза с января по июнь 2006 года (рисунок 7), нажмём кнопку ОК. Результаты прогнозирования представлены на рисунке 7 и 8.
Рисунок 7 – Прогнозирование временного ряда bezrob
For 95% confidence intervals, t(154,.025) = 1.975
Рисунок 8 – Результаты прогнозирования временного ряда bezrob Построим модель полиномиального тренда четвёртого порядка и сравним её с построенной моделью первого порядка. Просмотрим переменные t1,t2,t3 набора данных macro_1993_2005, дважды щёлкнув по их названию левой кнопкой мыши. Отметим, что t2= t12, а t3=t13. Для построения полинома четвёртого порядка, необходимо добавить переменную t4=t14 Щелчком мыши выберем переменную t2 в открытом наборе данных и обратимся ко команде Add\Squares of selected variables (рисунок 9), что добавит переменную sq_t2= t4=t14 к набору данных.
Рисунок 9 – Добавление переменной sq_t2
Повторим рассмотренную выше последовательность действий по построению линейного тренда, добавив в число объясняющих переменных t1,t2,t3, sq_t2 (рисунок 10). Окно результатов моделирования представлено на рисунке 11.
Рисунок 10 – Построение модели полиномиального тренда четвёртого порядка
Рисунок 11 – Окно результатов моделирования полиномиального тренда четвёртого порядка ряда bezrob
Повторим рассмотренную выше последовательность действий по прогнозированию рассматриваемого временного ряда (рисунок 11), составив прогноз на 1 месяц (рисунок 12). Для составления прогноза необходимо, чтобы переменные t1,t2,t3, sq_t2 не имели пустых значений на период составления прогноза. Просмотреть и заполнить недостающие значения данных переменных можно обратившись к команде View\Icon view и дважды щёлкнув левой кнопкой мыши по иконке Data set в режиме просмотра и редактирования набора данных. Полученная модель полиномиального тренда четвёртого порядка наилучшим образом описывает исходные данные, поскольку сумма квадратов ошибок RSS (Sum of squared residuals) для данной модели (136,489) существенно меньше данного значения для линейного тренда (928,949), в то время как коэффициент детерминации R2 (Unadjested R-quared), показывающий процент дисперсии bezrob, описанной моделью, напротив, значительно выше 88,71% >25,14%. При сравнении качества моделей также могут использоваться T- и F-критерии (большее значение критерия наиболее предпочтительное). Т.о. можно сделать вывод что построенная полиномиальная модель четвёртого порядка наиболее предпочтительна для прогнозирования рассматриваемого ряда, поэтому выбираем прогноз уровня безработицы в Польше на январь 2006 года равный 15,3257%согласно данной модели (рисунок 12). Реальный уровень безработицы в Польше в данный период составил 15%. For 95% confidence intervals, t(151,.025) = 1.976
Рисунок 12 – Результаты прогнозирования временного ряда bezrob с использование модели полиномиального тренда четвёртого порядка
|

 адекватна, параметры значимы (по t-критерию Стьюдента) на уровне 1%.
адекватна, параметры значимы (по t-критерию Стьюдента) на уровне 1%.