СВЯЗЬ ТЯГОТЕНИЯ С ГЕОМЕТРИЕЙ ПРОСТРАНСТВА
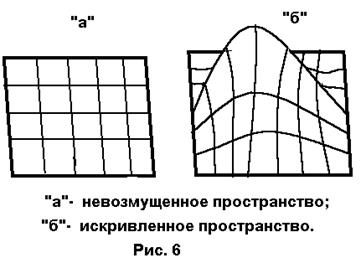
А теперь вспомним, что в соответствии с принципом Эйнштейна ускорение эквивалентно наличию тяготения. Следовательно, отклонение световых лучей, равно как и лучей, образованных потоками любых частиц, под влиянием тяготения неизбежно. Астрономические наблюдения подтверждают, что световые лучи отклоняются под влиянием тяготения в сторону солнца. В повседневной жизни мы пользуемся привычной нам геометрией Евклида, которая базируется на ряде постулатов, таких, как: сумма углов треугольника равна 180°; отношение длины окружности к ее диаметру равно числу p; через две точки можно провести только одну прямую линию; через точку, лежащую вне прямой, можно провести только одну прямую, параллельную данной... Геометрическую модель нашего пространства, обладающего евклидовыми свойствами, можно легко вообразить, если представить себе резиновую пленку с нанесенной на нее сеткой (Рис. 6 “а”).
Иллюстрация к идее связи между тяготением и геометрией
Но вот мы надавили пальцем на какой-то участок пленки (Рис. 6“б). Этот участок растянулся, изменились углы между линиями, сумма углов треугольника сделалась отличной от p, произошло нарушение Евклидовой геометрии. Отметим, что, чем ближе находится участок пленки к оказывающему давление пальцу, тем сильнее он искривляется. Между действием пальца и действием масс, вызывающих тяготение, можно провести аналогию. Ведь от действия пальца в одном месте в других местах пленки появляются упругие натяжения, которые так и хочется сравнить с гравитационными силами (они, кстати, убывают с расстоянием почти так же, как тяготение). Таким образом, мы с двух разных позиций - искривленного пространства и искривленных прямых пришли к выводу о неразрывной связи тяготения с геометрией. Для того, чтобы лучше понять этот неожиданный и ошеломляющий вывод, перенесемся мысленно на другую планету, где сила тяготения в десятки миллионов раз больше, чем наша. На такой планете направленный горизонтально луч света не сможет преодолеть притяжения и будет огибать планету параллельно ее поверхности как спутник. Если такой луч света послать с помощью прожектора на одном полюсе, то он, обогнув поверхность планеты, дойдет до второго полюса и, миновав его, вернется в эту же точку - только с другой стороны. Немного повернув прожектор, мы получим другой луч, другую прямую, также проходящую через оба полюса. Вывод: на этой планете через две точки - в данном случае через два полюса - можно провести бесчисленное множество прямых линий! Кстати, эти прямые будут иметь вид окружностей и на этой удивительной планете каждый человек безо всяких зеркал может увидеть свой собственный затылок. Вернемся, однако, на Землю и подведем итоги. Мы живем не в плоском, а в искривленном мире. Кривизна этого мира может дать иллюзию силы притяжения и эффект силы притяжения есть единственное, в чем такая кривизна может проявляться. Кривизна пространства (точнее следует говорить о кривизне пространства - времени) на Земле ничтожна, что позволяет применять на практике геометрию Евклида и приводит к малости гравитационных сил (сила взаимного притяжения двух людей среднего веса при расстоянии между ними в один метр не превышает 0,03 миллиграмма). Однако, несмотря на свою малую величину, гравитационные силы играют огромную роль в нашей жизни, о чем уже было сказано выше.
Законы гидростатики - физические соотношения между параметрами жидкости, при которых она остается неподвижной (в равновесии) под действием приложенных сил. К ним относятся: закон Гука, закон Паскаля, закон Архимеда и основное уравнение гидростатики, которое является следствием второго закона Ньютона. Поскольку задачи, основанные на применении закона Гука, имеют большее отношение к физическим свойствам жидкости, а не к инженерным гидростатическим расчетам, они в данном учебном пособии не рассматриваются. В этом разделе выведены указанные выше законы на основе простейших физических соображений и приведен ряд задач с подробным решением на применение этих законов.
|