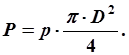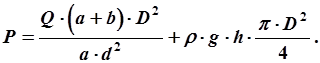Задача 1. . . Здесь р - давление в жидкости на горизонтальном уровне А-В, а p×D2/4- площадь большого поршня. 2. Для определения давления р используем условие равновесия жидкости
Решение. 1. Искомая сила Р равна:
Здесь р - давление в жидкости на горизонтальном уровне А-В, а p×D2/4- площадь большого поршня. 2. Для определения давления р используем условие равновесия жидкости: p = pA-B = pM-N + r×g×h; 3. Определяем давление на уровне M-N.
4. Для определения усилия F используем условие равновесия рычага: суммарный момент относительно точки поворота равен нулю - åM0=0. Согласно 3ему закону Ньютона, поршень 3 действует на рычаг 2 с силой, равной F, но направленной в другую сторону. Уравнение равновесия рычага имеет вид: F×a - Q×(a + b) = 0;
Из этого уравнения определяем силу F:
5. Подставляем выражения для силы F и давления на уровне M-N и получаем окончательную зависимость для силы прессования в виде:
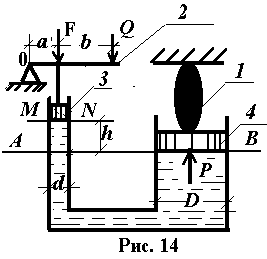
Нетрудно проверить при подстановке численных значений, что второе слагаемое пренебрежимо мало по сравнению с первым и его можно не учитывать. Итак: действуя на большее плечо рычага с силой Q, мы получаем механический выигрыш в силе (a+b)/a. Из-за разницы площадей поршней выигрыш в силе увеличивается пропорционально (D/d)2 (гидравлический выигрыш). Примечание: при решении задачи не учитывалось атмосферное давление, так как из Рис. 14 очевидно, что оно действует на поршень диаметра d, передается через жидкость на поршень диаметра D, действует на него снизу и сверху и таким образом уравновешивается.
|