Задача 1. .
Решение. 1. Высоту h0 определяем из условия, что сложное тело, состоящее из трубопровода диаметром d вместе с жидкостью и шарового клапана диаметром D находится в равновесии (плавает) в окружающей жидкости. Условие равновесия имеет вид (17): PZ =Gå Здесь Gå - суммарный вес клапана и трубопровода с жидкостью,
Поскольку в условии задачи вес самого трубопровода не задан, им можно пренебречь. Внимание! При определении веса жидкости пришлось ввести геометрический размер H, который не задан по условию. В дальнейшем величина H должна сократиться. Такой методический прием часто используется при решении задач. Выталкивающая сила PZ = r×g× VZ, где VZ - объем части нашего сложного тела, погруженной в жидкость, находящуюся в резервуаре. Он представляет собой сумму объемов цилиндра и шара:
2. Подставляем выражения для сил в уравнение равновесия и решаем его относительно h0.
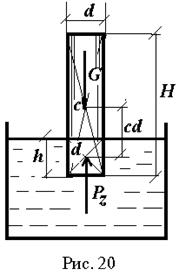
Задача решена. Задача 2 ( Рис.20). Решение. 1. Для определения двух неизвестных величин запишем два уравнения:
PZ =G (19) - условие равновесия тела; r ³ cd (20) - условие остойчивости.
Здесь: G =(rT×g×p×d2/4)×H - вес тела; PZ==(r×g×p×d2/4)×h - выталкивающая сила; cd= H/2- h/2 - расстояние между центром тяжести тела и центром водоизмещения.
Метацентрический радиус r равен: r = Минимальные значения плотности тела rTmin и глубины погружения hmin получаются из условия r = cd. В дальнейшем индекс “min” опускаем. 2. Решаем систему уравнений (19) ¸ (20):
Поверхности, на которые оказывает жидкость силовое воздействие, бывают плоские и криволинейные (рис 21.). Иллюстрация к появлению сил давления жидкости
На рис. 21”а”плоская крышка 1 закрывает отверстие в боковой стенке резервуара (форма отверстия может быть любая - круглая, прямоугольная и т.д.). Крышка 2 - криволинейная. Она является цилиндрической, если отверстие имеет форму прямоугольника, и сферической - если отверстие круглое. Крышка 3 - коническая, она закрывает круглое отверстие в стенке резервуара. Атмосферное давление действует на крышки снаружи и внутри, передаваясь через жидкость, и в результате не оказывает силового воздействия на крышки. Для расчета крепления крышек необходимо знать величину сил давления жидкости, которые для крышек 1 и 2 растягивают болты, а для крышки 3 - растягивают (сила Р3x) и срезают (сила Р3Z). Для определения направления сил необходимо вспомнить, что сила давления dP, действующая на элемент поверхности dw, направлена всегда перпендикулярно к нему (Рис. 21”б”). Чтобы определить суммарное воздействие, надо силы dP сложить геометрически. Поскольку для крышки 1 силы dPi горизонтальны, результирующая сила Р1 также будет горизонтальной. Вследствие симметрии горизонтальные составляющие сил dPi для крышки 2 уничтожаются и остается вертикальная сила Р2. В то же время для крышки 3 вертикальные составляющие на нижнюю часть будут больше, чем на верхнюю (чем глубже, тем больше давление в жидкости). В результате для крышки 3 получим горизонтальную силу Р3x и вертикальную силу Р3Z. А теперь рассмотрим ситуацию, когда резервуар закрыт и на поверхности жидкости давление больше атмосферного (показание манометра 4 равно рм, Рис.22).
Иллюстрация к появлению сил давления газа
Давление газа р0, равное (рат+р м), передается по закону Паскаля через жидкость и оказывает силовое воздействие на крышки изнутри. Вместе с тем снаружи на крышки действует атмосферное давление. В результате силы давления газа будут определяться через разницу давлений р0 и рат, то есть через давление рм и будут направлены изнутри наружу. В связи с тем, что давление газа одинаково во всех точках крышки, вертикальная составляющая силы давления на крышку 3 равна нулю. Если давление газа р0 меньше рат, силы давления газа будут направлены в противоположную сторону, то есть снаружи вовнутрь и будут прижимать крышки к стенке резервуара. Отметим, что результирующее воздействие на крышки будет складываться из силы давления жидкости и силы давления газа и равно геометрической сумме этих двух сил. При этом, когда давление газа меньше атмосферного, возможна гипотетическая ситуация, при которой крышки 1 и 2 будут удерживаться в равновесии без болтов. Для расчета крепления крышек, изображенных на Рис. 21, 22 достаточно знать величину и направление суммарной силы давления жидкости и газа. Далее выбрать материал для болтов, допускаемое напряжение, количество болтов и рассчитать их диаметр. Между тем для решения многих практических задач необходимо знать еще и точку приложения сил давления.
Иллюстрация к расчету стенки на опрокидывание
На Рис. 23 изображена ситуация, когда на перегораживающую поток жидкости стенку (плотину) действуют силы давления жидкости слева Р1 и справа P2 и собственный вес плотины G (силы изображены в проекции на плоскость чертежа). Эти силы создают вращающие моменты вокруг оси поворота 0-0. Если момент от силы Р1, равный Р1×x, будет больше, чем сумма моментов от сил G и Р2 (G×z+P2×y), стенка перевернется, в противном случае будет удерживаться в вертикальном положении. Для решения вопроса об устойчивости стенки необходимо знать точки приложения сил и их величину.
Резюме: Для решения практических задач необходимо уметь определять величину сил давления жидкости и газа, их направление и точки приложения.
|
I =×p×d4/64 - момент инерции круга диаметром d (сечение плавающего тела по ватерлинии есть круг, моменты инерции приведены в Приложении 1).
