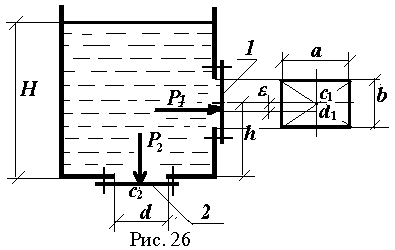
ПРИМЕР РАСЧЕТА
Решение. 1. Определяем модуль силы Р1 - силы давления жидкости на крышку Р1 =рс1×w1. Здесь: рс1= r×g× (H-h) - давление жидкости в центре тяжести с1 крышки 1, который расположен на глубине (H-h) под уровнем жидкости; w1 =a×b - площадь сечения крышки, которое смочено жидкостью. Отметим, что сама крышка по размерам больше, чем a×b, да и форма сечения всей крышки может быть иная, например, круглая. Жидкость же оказывает силовое воздействие только на ту часть поверхности крышки, которая находится с ней в контакте (на смоченную поверхность). Итак: Р1 = r×g× (H-h)× a×b - модуль силы Р1. 2. Определяем величину e - сдвиг точки приложения d1 силы Р1 относительно точки с1 - центра тяжести площади w1:
Здесь: Ic =a×b3/12 - момент инерции площади прямоугольника относительно горизонтальной оси (параллельной стороне а). Это справочная величина, (Приложение 1); lc1= H-h - расстояние от центра тяжести площади w1 до поверхности жидкости по оси симметрии крышки (в данном случае по вертикали); w1= a×b - площадь смоченной поверхности крышки.
3. Проводим вектор силы Р1 перпендикулярно крышке через точку d1. 4. Определяем модуль силы Р2 - силы давления жидкости на крышку2. Р2= рс2×w2 = r×g×H×p×d2/ 4. Здесь рс2 = r×g×H - давление в центре тяжести крышки, который расположен на глубине H под уровнем жидкости; w2=p×d2/ 4 - площадь смоченной поверхности крышки. 5. Определяем точку приложения силы Р2. Поскольку крышка 2 расположена горизонтально, давление жидкости одинаково во всех точках крышки и сила давления проходит через центр тяжести площади крышки. Внимание! Для горизонтальной поверхности центр тяжести и центр давления совпадают.
6. Проводим вектор силы Р2 через точку с2 перпендикулярно крышке.
|