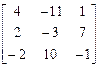Матричные операции
Простейшие операции, которые можно проделывать с матрицами: сложение (вычитание), умножение на число, перемножение, транспонирование, вычисление обратной матрицы. Упражнение 6.2.1. Сложение матриц. Задание. Сложить матрицы М и N, где
  и N= и N= 
1-й способ: § Ввести матрицу М в блок А1:С2, а матрицу N в блок Е1:G2. § В блок А4:С5 ввести табличную формулу {= А1:С2 + E1:G2}. G Примечание. Выделен блок, имеющий те же размеры, что и исходные матрицы. 2-й способ: Использование имен делает процедуру ввода табличной формулы намного проще: § Задать диапазонам А1:С2 и E1:G2 имена М и N. § В блок E4:G5 ввести табличную формулу { = М + N }. Результат, естественно, тот же: M+N = Упражнение 6.2.2. Вычислить линейную комбинацию матриц 2*М - N (матрицы М.и N из упражнения 6.2.1.). Решение. В блок А7:С8 ввести табличную формулу {= 2*М - N }. Результат: 2*M - N = Задача 6.2.1. Осмысленные результаты (не имеющие ничего общего с матричной алгеброй) получаются при сложении матриц разных размеров. Придумать примеры и попытаться выявить правила, по которым Excel выполняет такое сложение.
МОПРЕД — вычисление определителя матрицы; МОБР — вычисление обратной матрицы; МУМНОЖ — перемножение матриц; ТРАНСП — транспонирование. G Примечание. Первая из этих функций возвращает число, поэтому вводится как обычная формула. Остальные функции возвращают блок ячеек, поэтому они должны вводиться как табличные формулы.
А =
Решение. Разместить исходную матрицу в блоке А1:СЗ. 1) В ячейке Е2 поместить формулу для вычисления определителя = МОПРЕД (А1:СЗ). 2) В блок А5:С7 ввести формулу для вычисления обратной матрицы: - выделить блок А5:С7 (он имеет три строки и три столбца, как и исходная матрица). - Ввести формулу {=МОБР (А1:СЗ)}. G Примечания: a) При использовании Мастера функций нужно завершать ввод нажатием комбинации клавиш Ctrl+Shift+Enter (вместо щелчка по кнопке "ОК"). b) Для удобства работы рекомендуется задавать имена исходной матрице и обратной матрице. 3) Проверить правильность вычисления обратной матрицы умножением ее на исходную: - задать имена исходной матрице - А и обратной матрице - АО; - в блок D5:F7 ввести формулу {=МУМНОЖ (А,АО)}. -
Рис. 16. Иллюстрация к упражнению 6.2.3.
В блок А9:С11 ввести табличную формулу {= abs (A-AО)}.
Задача 6.2.2. При каком значении элемента а33 определитель матрицы А обратится в нуль. Задача 6.2.3. Дана матрица S = Е — единичная матрица. Задача 6.2.4. Вычислить обратную матрицу для и применить форматирование, чтобы элементы матрицы представляли собой правильные дроби. Выбрать формат на основе величины определителя матрицы.
G Набор матричных операций в Excel беден. Если нужно серьезно работать с матрицами, лучше прибегнуть к помощи таких математических пакетов, как MatLAB (Matrix LABoratory), Mathematica, Derive.
|




 Для матричных операций в Excel предусмотрены функции, входящие в категорию "Математические":
Для матричных операций в Excel предусмотрены функции, входящие в категорию "Математические":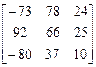 Упражнение 6.2.3. Вычислить определитель и обратную матрицу для матрицы:
Упражнение 6.2.3. Вычислить определитель и обратную матрицу для матрицы: как и следовало ожидать, получилась матрица, близкая к единичной.
как и следовало ожидать, получилась матрица, близкая к единичной.


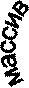
 . Вычислить матрицу 2SSТ - Е, где Т — операция транспонирования,
. Вычислить матрицу 2SSТ - Е, где Т — операция транспонирования,