Лабораторная работа № 3 по теме
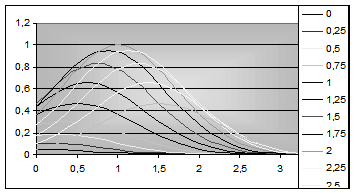
"Адресация" и "Диаграммы"; 1. Табулирование функции. Задание 3.1. 1) Рассчитать таблицу значений функции f(x)= 2) Вывести значения функции в n точках этого интервала. 3) Построить график функции. 4) Изменяя значения a, b, n, проследить за изменением функции по её графику. Выполнение. 1. Задать а= - 2. Вычислить шаг изменения функции по формуле: шаг =(b-а)/ n 3. Вычислить значения аргумента х: Точка 1 - х = а (формула в ячейке B7: =С2); Точка 2 - х = а + шаг (формула в В8: = B7+C$5); формула из ячейки В8 копируется на блок ячеек В9:В17. 4. Вычислить значения функции F(x) по формуле: = 4*EXP(-ABS(B7))-1, формула из ячейки С7 копируется на блок С8:С17. 5. Диаграмму оформить с помощью Мастера диаграмм.
Рис.10. Иллюстрация к заданию 3.1. 2. Решение нелинейного уравнения Задание 3.2. Решить уравнение f(x)= G Напоминание. 1. Решить уравнение f(x) = 0 означает: найти значения аргумента х, при которых функция f(x) обращается в 0. 2. Решить уравнение графическим способом: найти точки пересечения графика функции с осью ОХ. Решение. 1) Определить приближённые значения отрезка ОХ, в котором могут быть корни заданного уравнения. 2) Протабулировать функцию f(x)= 3) Построить график функции по полученным табличным значениям. G Примечание. Для заданной функции первые три пункта решения выполнены в предыдущем задании 3.1. 4) Из графика следует, что функция в заданном отрезке [- Уточнить последовательно оба корня: · задать значения а= -1.8, b = -1.2 (в этом отрезке функция переходит через 0). Обратить внимание на изменения в графике и табличные значения f(x). Если полученная точность (f(x)=0 с точностью 0.0063) вас устраивает, то первым корнем уравнения можно считать значение х1=-1.38. · Если полученная точность не подходит, то нужно задать новые значения а и b (а= -1.39, b = -1.37). Получается f(x)=0.003 в точке 3, при х= -1.386. · Второй корень находится аналогичным образом. Функция симметрична относительно х=0, поэтому х2=1.386
Задание 3.3. Решить уравнение f(x)= Решение. с помощью итераций § Установить в ячейке С47 любое начальное значение х из отрезка [-2; 0]. § Выделить ячейку D47, в которой вычисляется F(x). § Выполнить команду " Сервис/ Подбор параметра ". В диалоговом окне поле "Установить в ячейке:" уже содержит адрес выделенной ячейки D47. - в поле "Значение:" ввести 0, - в поле "Изменяя значение ячейки:" ввести адрес ячейки C47, содержащей величину x, "ОК". § Выводится новое окно "Результаты подбора параметра" c найденным решением. §
3. Построение поверхности сложной функции Задание 3.4. Построить поверхность по формуле:
Построить сечения и линии уровня[4] поверхности. § ввести значения х в столбец А, начиная с А2, автозаполнением с нуля c шагом 0,25 до х=4; § ввести значения y в строку 1, начиная с В1, автозаполнением с нуля c шагом 0,25 до y=3; § В В2 ввести формулу: EXP(-((A2-2)^2-(A2-2)*(B1-1)+(B1-1)^2)); § адресам А2 и В1 задать необходимый для копирования формулы по строкам и столбцам тип адресации; § скопировать формулу из ячейки В2 на всю таблицу с заданным диапазоном x и y; § выделить всю таблицу, включая значения x и y, и построить диаграмму типа " поверхность "; § изменить ракурс просмотра диаграммы -«ухватить» угол (+)
Рис.12. Поверхность задания 3.4 § Построение линий уровня поверхности - тип диаграммы - "поверхность", проволочная контурная диаграмма (рис. 13а). §
б)
а)
Рис.13. Способы представления поверхности: а) линии уровня; б) нормальные сечения
|

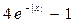 , где x меняется от a до b.
, где x меняется от a до b.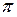 , b =
, b = 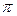 , n =10. Ввести эти значения в соответствующие ячейки, при вводе
, n =10. Ввести эти значения в соответствующие ячейки, при вводе 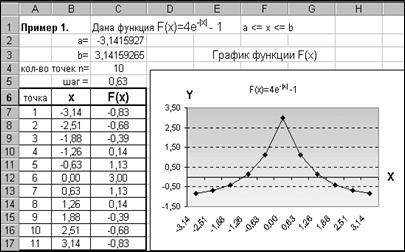
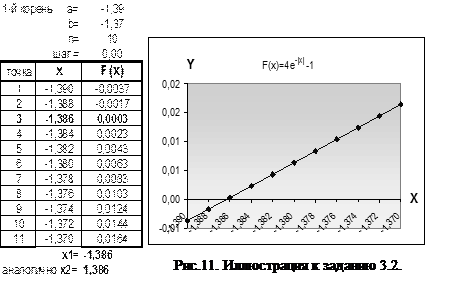
 Аналогичным образом найти 2-й корень уравнения.
Аналогичным образом найти 2-й корень уравнения. 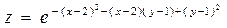 для х
для х 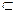 [0,4] и y
[0,4] и y 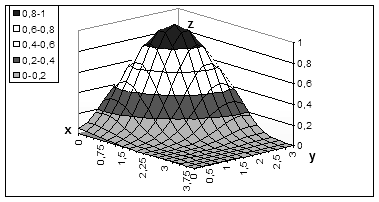
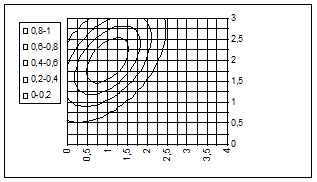 для построения сечений задать тип диаграммы - "точечная" без маркеров (рис. 13б);
для построения сечений задать тип диаграммы - "точечная" без маркеров (рис. 13б);