Определение преобразования Фурье

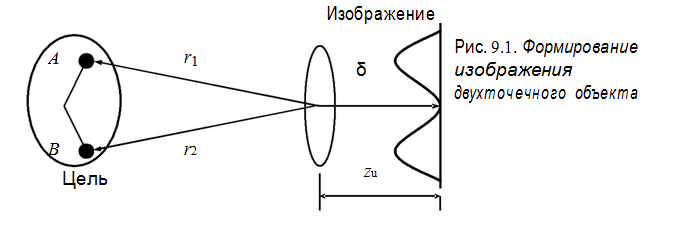
Анализ Фурье и теория линейных систем образуют фундамент, на котором построены теории формирования изображения, оптической обработки информации и голографии.

По определению преобразованием Фурье функции f (x) (действительной или комплексной) называется интегральная операция .Преобразование такого вида представляет собой функцию независимой переменной u, называемой частотой. Обратное преобразование Фурье функции F (u) записывается следующим образом .Необходимым условием существования преобразования Фурье является абсолютная интегрируемость функций f (x) и F (u), т.е. чтобы значения интегралов

были конечными. Функции, используемые в оптике, определены лишь на ограниченном интервале и для них это требование соблюдается всегда (переменные x и u называются сопряженными). Различия между прямым Фурье-образом и обратным Фурье-образом заключается в различных знаках, содержащихся в экспонентах выражений, а также в наличии множителя 1/2π в формуле обратного преобразования.

В литературе встречаются и другие определения преобразования Фурье, отличающиеся от приведенного здесь как знаком в экспоненте, так и численными коэффициентами, стоящими перед интегралом.

Аналогичным образом определяется и двумерное Фурье-преобразование.

Прямое (1.1)

и обратное

Введем в выражении (1.1) обозначения u = x /λz; v = y/λz.

Величины u и v обычно называются частотами. Тогда выражение (1.1) примет вид

где

Отсюда видно, что выражение (1.1) с точностью до множителя представляет собой Фурье-образ распределения поля на поверхности σ как функцию пространственных частот u и v. Аналогичным образом можно преобразовать и выражение для сферической системы координат, введя обозначения

Большое распространение имеет и частный случай двумерного преобразования Фурье для функций, обладающих осевой симметрией, называемый преобразованием Фурье-Бесселя или преобразованием Ганкеля нулевого порядка. Если функция обладает осевой симметрией ее можно записать как функцию только радиуса r. Соответственно, Фурье-образ становится функцией ρ, не зависящей явно от угла ϕ.

где J ₀(2π r ρ) - функция Бесселя первого рода нулевого порядка.

Учитывая, что

прямое преобразование Фурье можно записать в виде суммы косинус - и синус - преобразований:

В общем случае функция F (u, v) комплексная, и мы можем записать

Спектр амплитуд и фаз записывается соответственно в виде

Действительная часть Фурье-образа всегда четная функция, мнимая часть Фурье-образа - всегда нечетная функция. Комплексность спектра означает сдвиг отдельных его составляющих по фазе.

54.Статистические характеристики когерентных изображений.

Рассмотрим свойства когерентного изображения для случая, когда цель подсвечивается когерентным излучением, и состоит из двух точечных объектов (Рис. 9.1.). Зададим расположение этих объектов с помощью радиус-векторов r ₁ =(x ₁, y ₁, z ₁ ), r ₂ =(x ₂, y ₂, z ₂ ). И пусть изображение этого объекта строится тонкойлинзой.

Линза, формирующая изображение, имеет фокусное расстояние f: 1 /f= 1 /r_ц+ 1 /z_и. В этом случае поле в изображении представляется в виде сумм двух слагаемых, соответствующих изображению двух точечных объектов:

 

E (δ) ~ k ₁ A ′(δ)+ k ₂ B ′(δ),

 

где k ₁, k ₂ – коэффициенты отражения от точечных объектов A и B; δ - радиус вектор изображения.

 

На рис. 9.2 приведены построенные при различных реализациях x ₁, x ₂ изображения для случая плоского экрана.

Видно, что распределение интенсивности I(δ) = ⎪E(δ)⎪2 существенно зависит как от k1, k2, и от x1, x2.

Естественно считать k1 ≈ k2. Если выполняется условие x1 - x2 < λrц /dρ, то при k1 ≈ k2 отклики от обоих точечных объектов располагаются практически в одном месте.

Когерентные изображения объектов, состоящих из точек с достаточно

большим случайным разбросом расстояний между ними, сильно флуктуируют,

т.е. представляют собой сильно изрезанные по яркости структуры.

Можно предположить, что при увеличении числа точек, составляющих

подобные объекты, контраст будет увеличиваться.

Контраст в когерентном изображении многоточечного объекта, состоящего из случайно и независимо расположенных точек, разброс по фазе которых существенно превышает длину волны подсвечивающего излучения, стремится к единице