Теория когерентных изображений
Рассмотрим свойства когерентного изображения для случая, когда цель подсвечивается когерентным излучением, и состоит из двух точечных объектов (Рис. 9.1.). Зададим расположение этих объектов с помощью радиус-векторов r1=(x1, y1, z1), r2=(x2, y2, z2). И пусть изображение этого объекта строится тонкой линзой.
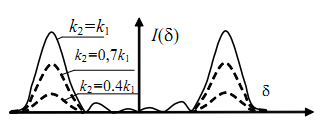
Рис. 9.1. Формирование изображения двухточечного объекта Линза, формирующая изображение, имеет фокусное расстояние f: где k1, k2 – коэффициенты отражения от точечных объектов A и B; δ - радиус вектор изображения. На рис. 9.2 приведены построенные при различных реализациях x1, x2 изображения для случая плоского экрана.
Рис. 9.2. Распределение интенсивности в когерентном изображении двухточечного объекта Видно, что распределение интенсивности I(δ) = ⎪E(δ)⎪2 существенно зависит как от k1, k2, и от x1, x2. Естественно считать k1 ≈ k2. Если выполняется условие x1 - x2 < λrц /dρ, то при k1 ≈ k2 отклики от обоих точечных объектов располагаются практически в одном месте. Когерентные изображения объектов, состоящих из точек с достаточно большим случайным разбросом расстояний между ними, сильно флуктуируют, т.е. представляют собой сильно изрезанные по яркости структуры. Можно предположить, что при увеличении числа точек, составляющих подобные объекты, контраст будет увеличиваться. Контраст в когерентном изображении многоточечного объекта, состоящего из случайно и независимо расположенных точек, разброс по фазе которых существенно превышает длину волны подсвечивающего излучения, стремится к единице.
|


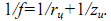 . В этом случае поле в изображении представляется в виде сумм двух слагаемых, соответствующих изображению двух точечных объектов
. В этом случае поле в изображении представляется в виде сумм двух слагаемых, соответствующих изображению двух точечных объектов 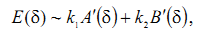 ,
,