Напряжения и деформации при кручении круглого вала.
Расчет на прочность и жёсткость Рассмотрим брус круглого сечения, нагруженный парами сил в плоскости торцевого сечения (рис.7.7). В поперечных сечениях этого бруса возникает постоянный крутящий.момент мя сечениями в процессе деформации кручения не изменяется (εz = 0); 3) поперечные сечения в своей плоскости не деформируются, т.е., радиусы не искривляются и не изменяют своей длины, они лишь поворачиваются как жесткие диски (εх=0, εу=0). На основании этих допущений σх =σу =σz =τху =0, поэтому в поперечных сечениях будут действовать только касательные напряжения τzx и τzу, следовательно, при кручении брус испытывает деформацию чистого сдвига. Двумя поперечными сечениями выделим из вала элемент длиной dz, а из него затем выделим элементарное кольцо с радиусами ρ и ρ + dρ (рис. 7.8). Будем считать левое торцевое сечение неподвижным, тогда правое торцевое сечение кольца повернется под действием крутящего момента относительно левого на угол dφ. Образующая цилиндра АВ при этом повернётся на угол γ и займет положение
Угол γ – это угол сдвига цилиндрической поверхности, а величина

Так как
Из последнего выражения следует формула угла закручивания
Если крутящий момент Мк и жесткость вала GІρ по его длине не изменяются, то
  (7.9) (7.9)
Согласно этой формуле касательные напряжения в поперечном сечении вала распределяются вдоль радиуса по линейному закону, достигая наибольшей величины в точке наиболее удаленной от оси бруса (рис.7.9). Согласно (7.10): Введя обозначение
Для круглого сечения
Материал вала возле оси недогружен, поэтому применяют пустотелые валы. При равных площадях поперечных сечений и одинаковом крутящем моменте в пустотелом вале напряжения будут меньше, а при равных напряжениях в пустотелом вале крутящий момент будет больше. Для такого вала где D- наружный диаметр, d – внутренний диаметр вала,
Расчёт на прочность круглого вала может выполняться по двум методам: по допус-каемым напряжениям и по допускаемым нагрузкам. В данном разделе рассмотрим первый метод- метод допускаемых напряжений, так как он наиболее часто используется на практике.
 Предельное состо-яние в опасной точке, расположенной на повер-хности вала (рис.7.10) достигается в сечении с наибольшим крутящим моментом. В этой точке будет напряжённое сос-тояние чистого сдвига, т.е. по граням элементарного параллелепипеда действу-ют только касательные напряжения (рис.7.11). В этом случае Предельное состо-яние в опасной точке, расположенной на повер-хности вала (рис.7.10) достигается в сечении с наибольшим крутящим моментом. В этой точке будет напряжённое сос-тояние чистого сдвига, т.е. по граням элементарного параллелепипеда действу-ют только касательные напряжения (рис.7.11). В этом случае 
состояния определяется выражением
Для рассматриваемого случая оно примет вид Для безопасной работы вала должно выполняться условие
Таким образом, условие прочности при кручении круглого вала запишется формулой:
Из него следуют формулы для назначения размеров поперечного сечения вала и определения грузоподъёмности:
Условие жесткости Произведение GIρ называется жесткостью при кручении. Іρ – полярный момент инерции, G – модуль упругости при сдвиге. Если вал имеет несколько участков, то угол закручивания φ на всей его длине найдется как сумма углов закручивания на всех участках φi: φ =∑ φi =∑ Пример: подобрать размеры круглого и кольцевого сечения вала, передающего мощ-ность 80 кВт при числе оборотов n=600об/мин, если Мк = Для круглого сечения: площадь сечения А = Для кольцевого сечения:
Массы валов будут пропорциональны площадям поперечных сечений
|


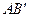 . С одной стороны дуга
. С одной стороны дуга  / =ρdφ, с другой - В/ В/ = γdz, следовательно,
/ =ρdφ, с другой - В/ В/ = γdz, следовательно, . (7.6)
. (7.6) Θ называется относительным углом закручивания (аналогично
Θ называется относительным углом закручивания (аналогично 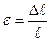 ).
).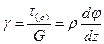 ,
откуда следует
,
откуда следует
 (7.7)
Подставляя (7.7) в уравнение (7.5), получим
(7.7)
Подставляя (7.7) в уравнение (7.5), получим 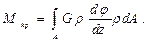
 , то
, то 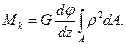 Учитывая, что
Учитывая, что  получим
получим ,
,  (а),
(а),  .
.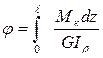 (7.8)
(7.8) Вернёмся к выражению (7.7). Используя уравнение (а), получим формулу касательных напряжений при кручении круглого вала
Вернёмся к выражению (7.7). Используя уравнение (а), получим формулу касательных напряжений при кручении круглого вала
 =
=  (7.10)
(7.10) или
или  .
. (момент сопротивления сечения при кручении), получим
(момент сопротивления сечения при кручении), получим .
.
 ,
, ,
,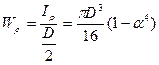 .
.
 .
.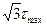 =
=  .
. ,т.е.
,т.е. , где
, где  .
. . (7.11)
. (7.11) ,
,  (7.12)
(7.12) . (7.13)
. (7.13) (7.14)
(7.14) , α =
, α =  . Сравнить массы валов с указанными сечениями.
. Сравнить массы валов с указанными сечениями. ,
,  .
. , тогда
, тогда  ,
, .
. ,
,  ,
, , площадь сечения А=
, площадь сечения А=  .
. , т.е., полый вал будет почти в два раза легче сплошного вала.
, т.е., полый вал будет почти в два раза легче сплошного вала.


