Кручение тонкостенного стержня с замкнутым профилем
Рассмотрим кручение стержня с поперечным сечением в форме тонкостенного замкнутого профиля (рис.7.16). В этом стержне, в отличие от открытого профиля, напряжения по толщине стенки распределяютя равномерно. Выделим из этого стержня элементарный объём длиной dz, расстояние между точками 1 и 2 которого произвольное. Пусть толщина контура в точке 1 будет δ1, а в точке 2 – δ2. Обозначим соответственно через τ1 и τ2 напряжения в поперечном сечении. В продольных сечениях будут действовать парные напряжения
Составим для рассматриваемого элемента уравнение равновесия, спроектировав все силы на направление оси стержня
Из полученного равенства следует, что τδ = const, так как точки 1 и 2 взяты произвольно. Таким образом, произведение τδ по длине замкнутого контура является величиной постоянной. На участках с меньшей толщиной напряжения будут соответственно бòльшими. Выразим крутящий момент через напряжения τ. Для этого возьмём на контуре элементарную дугу длиной ds (рис. 7.17). Момент силы τ·δ·ds относительно произвольной точки О равен τδds|ОА|. Тогда Мк = ∫ Так как τδ по длине дуги не изменяется, то получим Мк = τδ ∫ Выражение Мк = τδ2 F*. наибольшее напряжение
Для определения углового перемещения φ рассмотрим соотношение потенциальной энергии, выраженной через напряжения τ и выраженной через внешний момент М. Удельная потенциальная энергия при сдвиге определяется выражением
Энергия, накопленная в элементарном объёме с размерами ds, z, δ равна
dU = Это выражение необходимо проинтегрировать по длине стержня и по дуге замкнутого контура U = Последний интеграл зависит от закона изменения толщины по дуге контура и является геометрической характеристикой сечения. Учитывая, что τδ = Получим U = Теперь эту же энергию найдём как работу внешнего момента М на угловом перемещении φ:
U= Из равенства этих двух выражений находим
Если толщина δ по дуге контура не меняется, то
где s - длина замкнутого контура. Для рассмотренного тонкостенного замкнутого профиля вводятся геометрические параметры Wk, Ik, которые согласно полученным формулам для вычислений напряжений углов поворотов определятся выражениями:
Теперь формулы для вычислений напряжений углов поворотов примут вид:
Контрольные вопросы 1. Когда брус испытывает кручение? 2. Что называется валом? 3. Какие внутренние усилия действуют в поперечном сечении вала? Как они определяются? 4. Какие напряжения действуют в поперечном сечении вала? 5. Как определяются максимальные напряжения в поперечном сечении вала? 5. Условие прочности при кручении вала? 6. Какие перемещения возникают в вале при кручении и как они определяются? 7. Как определяется жёсткость при кручении вала?
|

 .
.
 .
. .
. .
. представляет собой удвоенную площадь треугольника ОВС, а интеграл от этого произведения по длине замкнутого контура даёт удвоенную площадь, ограниченную средней линией контура. Обозначим эту площадь через F*. Таким образом,
представляет собой удвоенную площадь треугольника ОВС, а интеграл от этого произведения по длине замкнутого контура даёт удвоенную площадь, ограниченную средней линией контура. Обозначим эту площадь через F*. Таким образом, .
. .
. .
. .
.
 .
. .
. .
.
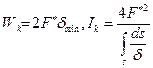 .
.



