 Рассмотрим нагружение прямого шарнирно закреплённого стержня продольной силой F и системой поперечных сил. Такой вид нагружения принято называть продольно- поперчным изгибом. Обозначим у(z) прогиб балки в сечении c абсциссой z. Воспользуемся дифференциальным уравнением упругой линии балки, в котором изгибающий момент можно рассматривать как сумму моментов поперечных сил
Рассмотрим нагружение прямого шарнирно закреплённого стержня продольной силой F и системой поперечных сил. Такой вид нагружения принято называть продольно- поперчным изгибом. Обозначим у(z) прогиб балки в сечении c абсциссой z. Воспользуемся дифференциальным уравнением упругой линии балки, в котором изгибающий момент можно рассматривать как сумму моментов поперечных сил  и момента продольной силы F·y. Полный прогиб у складывается из прогиба уп от поперечных сил и дополнительного прогиба у-уп от осевой силы F. Полный прогиб у больше суммы прогибов, возникающих при раздельном действии поперечных и продольных сил, так как при действии только силы F прогиб равен нулю. Следовательно, в данном случае принцип независимости действия сил не применим.
и момента продольной силы F·y. Полный прогиб у складывается из прогиба уп от поперечных сил и дополнительного прогиба у-уп от осевой силы F. Полный прогиб у больше суммы прогибов, возникающих при раздельном действии поперечных и продольных сил, так как при действии только силы F прогиб равен нулю. Следовательно, в данном случае принцип независимости действия сил не применим.
 (8.5).
(8.5).
Разделим левую и правую части выражения (9.5) на EI:
 (8.6)
(8.6)
Так как  , то подставив это значение в (8.6), получим
, то подставив это значение в (8.6), получим
 ,
,
или
 (8.7).
(8.7).
Для упрощения решения предполагается, что дополнительный прогиб  по длине балки изменяется по синусоиде, т.е.
по длине балки изменяется по синусоиде, т.е.
 (8.8).
(8.8).
Это допущение позволяет получить точные результаты при действии на балку поперечной нагрузки, направленной в одну сторону.
С учётом (8.8) выражение (8.7) примет вид
: 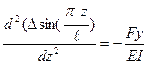 .
.
После двухкратного дифференцирования этого уравнения получим
 ,
,
или  .
.
Из этого равенства на ходим
 .
.
Выражение  =Fэ совпадает в формулой Эйлера, тогда
=Fэ совпадает в формулой Эйлера, тогда
у=  (8.9)
(8.9)
Необходимо отличать эйлерову силу Fэ от критической силы Fкр, вычисляемой по формуле Эйлера для стержней большой гибкости ( ). Эйлерова сила Fэ не зависит от гибкости стержня.
). Эйлерова сила Fэ не зависит от гибкости стержня.
Из формулы (8.9), что отношение 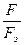 является критерием жесткости при продольно поперечном изгибе. Если
является критерием жесткости при продольно поперечном изгибе. Если 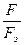 → 0, жёсткость балки велика и
→ 0, жёсткость балки велика и 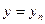 . При
. При 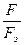 → 1 жёсткость мала, балка очень гибкая и у→ ∞, т.е., прогибы многократно возрастают по сравнению с
→ 1 жёсткость мала, балка очень гибкая и у→ ∞, т.е., прогибы многократно возрастают по сравнению с 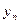 .
.
Формула (8.9) достаточно точная при F≤Fкр.
Расчёт на прочность при продольно – поперечном изгибе
Условие прочности при поперечном изгибе  получено в предположении, что внутренние усилия
получено в предположении, что внутренние усилия  изменяются пропорционально изменению внешних сил. Как установлено ранее, при продольно-поперечном изгибе эта зависимость нелинейная.
изменяются пропорционально изменению внешних сил. Как установлено ранее, при продольно-поперечном изгибе эта зависимость нелинейная.
Предполагая, что моменты пропорциональны прогибам, можно записать
 (8.10)
(8.10)
Будем считать, что при переходе к предельному состоянию внешние нагрузки возрастают пропорционально, тогда справедливы отношения
 (8.11)
(8.11)
Здесь  и
и  нагрузки, при которых в балке напряжения достигают предела текучести
нагрузки, при которых в балке напряжения достигают предела текучести
( ). Из (8.11) следует
). Из (8.11) следует  .
.
Наибольшие напряжения при поперечном изгибе с растяжением вычисляются по формуле
 =
= 
 .
.
При достижении предельного состояния они будут равны
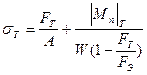 =
=  .
.
Разделив правую и левую часть этого уравнения на коэффициент запаса по текучести  , получим
, получим
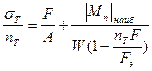 .
.
Так как  , то условие прочности при продольно-поперечном изгибе примет вид
, то условие прочности при продольно-поперечном изгибе примет вид


 . (8.12)
. (8.12)
Нелинейность в этом выражении определяется коэффициентом  . За счёт этой нелинейности левая часть условия прочности будет несколько меньше.
. За счёт этой нелинейности левая часть условия прочности будет несколько меньше.

 Рассмотрим нагружение прямого шарнирно закреплённого стержня продольной силой F и системой поперечных сил. Такой вид нагружения принято называть продольно- поперчным изгибом. Обозначим у(z) прогиб балки в сечении c абсциссой z. Воспользуемся дифференциальным уравнением упругой линии балки, в котором изгибающий момент можно рассматривать как сумму моментов поперечных сил
Рассмотрим нагружение прямого шарнирно закреплённого стержня продольной силой F и системой поперечных сил. Такой вид нагружения принято называть продольно- поперчным изгибом. Обозначим у(z) прогиб балки в сечении c абсциссой z. Воспользуемся дифференциальным уравнением упругой линии балки, в котором изгибающий момент можно рассматривать как сумму моментов поперечных сил  и момента продольной силы F·y. Полный прогиб у складывается из прогиба уп от поперечных сил и дополнительного прогиба у-уп от осевой силы F. Полный прогиб у больше суммы прогибов, возникающих при раздельном действии поперечных и продольных сил, так как при действии только силы F прогиб равен нулю. Следовательно, в данном случае принцип независимости действия сил не применим.
и момента продольной силы F·y. Полный прогиб у складывается из прогиба уп от поперечных сил и дополнительного прогиба у-уп от осевой силы F. Полный прогиб у больше суммы прогибов, возникающих при раздельном действии поперечных и продольных сил, так как при действии только силы F прогиб равен нулю. Следовательно, в данном случае принцип независимости действия сил не применим. (8.5).
(8.5). (8.6)
(8.6) , то подставив это значение в (8.6), получим
, то подставив это значение в (8.6), получим ,
, (8.7).
(8.7). по длине балки изменяется по синусоиде, т.е.
по длине балки изменяется по синусоиде, т.е. (8.8).
(8.8).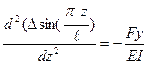 .
. ,
, .
. .
. =Fэ совпадает в формулой Эйлера, тогда
=Fэ совпадает в формулой Эйлера, тогда (8.9)
(8.9) ). Эйлерова сила Fэ не зависит от гибкости стержня.
). Эйлерова сила Fэ не зависит от гибкости стержня.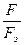 является критерием жесткости при продольно поперечном изгибе. Если
является критерием жесткости при продольно поперечном изгибе. Если 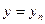 . При
. При 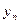 .
. получено в предположении, что внутренние усилия
получено в предположении, что внутренние усилия  (8.10)
(8.10) (8.11)
(8.11) и
и  нагрузки, при которых в балке напряжения достигают предела текучести
нагрузки, при которых в балке напряжения достигают предела текучести ). Из (8.11) следует
). Из (8.11) следует  .
. =
= 
 .
.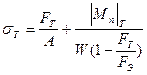 =
=  .
. , получим
, получим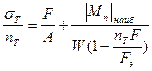 .
. , то условие прочности при продольно-поперечном изгибе примет вид
, то условие прочности при продольно-поперечном изгибе примет вид

 . (8.12)
. (8.12)


