Зависимость между упругими характеристикамиматериала E, G и μ;
Эту же энергию деформации выразим через главные напряжения
При чистом сдвиге следует
КРУЧЕНИЕ Основные понятия Будем рассматривать прямой брус постоянного сечения. Такой брус испытывает кручение, если он нагружен парами сил, плоскость действия которых перпендикулярна его оси. Брус, испытывающий деформацию кручения, называется валом.
Равновесие правой части (рис.7.5, b): Из полученных выражений следует, что крутящий момент в любом сечении равен сумме моментов внешних пар сил, расположенных по одну сторону от сечения. При этом принимаются следующие правила знаков: если смотреть на сечение со стороны внешней нормали то крутящий момент принимается положительным, если он направлен против хода часовой стрелки, и отрицательным, если направлен по ходу часовой стрелки. Эпюра крутящих моментов Мк – это график изменения его величины вдоль оси вала (рис.7.6).
|
работа сил (А), действующих по граням выделенного объёма (рис.7.4) переходит в энергию деформации (U): A=U= 
, здесь 
- сила, действующая на грани рассматриваемого объёма, αγ=δ – перемещение, на котором совершается работа. Так как 
, то энергия деформации определится выражением 
, а удельная энергия деформации выражением 
u= 
, так как 
, то 
(а).
.
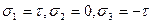, то 
(б). Из равенств (а) и (б)
. (7.3)
, 
