В расчётах на устойчивость необходимо рассмотреть два условия. Условие прочности
при сжатии  (α) и условие устойчивости
(α) и условие устойчивости 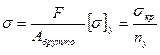 (b). Здесь
(b). Здесь  - напряжение предельного состояния. Если разделим равенство (b) на (α)
- напряжение предельного состояния. Если разделим равенство (b) на (α)  , то получим
, то получим  . Введём обозначение
. Введём обозначение  ,
,
полученный коэффициент  называется коэффициентом снижения допускаемых напряжений. Теперь условие устойчивости примет вид
называется коэффициентом снижения допускаемых напряжений. Теперь условие устойчивости примет вид  . Коэффициент
. Коэффициент  зависит от гибкости стержня и от материала, а его значения приводятся в виде таблиц или графиков.
зависит от гибкости стержня и от материала, а его значения приводятся в виде таблиц или графиков.
Существует два вида расчёта на устойчивость- проверочный и проектировочный.
Проверочный расчёт:
-известны форма сечения и его размеры, определяются площадь сечения А, момент инерции Imin, радиус инерции  , гибкость стержня λ
, гибкость стержня λ  ;
;
-по таблицам находится  ;
;
-вычисляется допускаемое напряжение 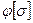 ;
;
-сравнивается напряжение в стержне с допускаемым 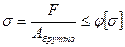 .
.
Проектировочный расчёт.
Известны форма сечения и действующая нагрузка, требуется определить размеры поперечного сечения.
Из условия устойчивости 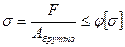 записывается выражение для площади поперечного сечения
записывается выражение для площади поперечного сечения  , в котором неизвестны две величины – Абрутто и
, в котором неизвестны две величины – Абрутто и  . Задача в этом случае задача решается методом последовательных приближений, в каждом из которых выбирается новое значение
. Задача в этом случае задача решается методом последовательных приближений, в каждом из которых выбирается новое значение  .
.
В первой попытке наиболее часто принимают  , определяется
, определяется  , вычисляются
, вычисляются 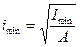 и
и 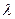
 , по таблице находится фактическое значение
, по таблице находится фактическое значение  . Если
. Если  значительно отличается от
значительно отличается от  , то и напряжение σ будет значительно отличаться от допускаемого. Тогда во второй попытке принимается
, то и напряжение σ будет значительно отличаться от допускаемого. Тогда во второй попытке принимается  . В рассмотренном ранее порядке вновь находится фактическое значение
. В рассмотренном ранее порядке вновь находится фактическое значение  Если отличие от рабочего напряжения от допускаемого больше 3…5%, то выполняется третья попытка
Если отличие от рабочего напряжения от допускаемого больше 3…5%, то выполняется третья попытка  .
.
Обычно требуется не более двух-трёх попыток.

 (α) и условие устойчивости
(α) и условие устойчивости 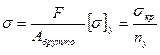 (b). Здесь
(b). Здесь  - напряжение предельного состояния. Если разделим равенство (b) на (α)
- напряжение предельного состояния. Если разделим равенство (b) на (α)  , то получим
, то получим  . Введём обозначение
. Введём обозначение  ,
, называется коэффициентом снижения допускаемых напряжений. Теперь условие устойчивости примет вид
называется коэффициентом снижения допускаемых напряжений. Теперь условие устойчивости примет вид  . Коэффициент
. Коэффициент  , гибкость стержня λ
, гибкость стержня λ  ;
; ;
;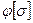 ;
;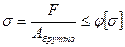 .
. , в котором неизвестны две величины – Абрутто и
, в котором неизвестны две величины – Абрутто и  . Задача в этом случае задача решается методом последовательных приближений, в каждом из которых выбирается новое значение
. Задача в этом случае задача решается методом последовательных приближений, в каждом из которых выбирается новое значение  , определяется
, определяется 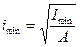 и
и 
 . Если
. Если  , то и напряжение σ будет значительно отличаться от допускаемого. Тогда во второй попытке принимается
, то и напряжение σ будет значительно отличаться от допускаемого. Тогда во второй попытке принимается  . В рассмотренном ранее порядке вновь находится фактическое значение
. В рассмотренном ранее порядке вновь находится фактическое значение  Если отличие от рабочего напряжения от допускаемого больше 3…5%, то выполняется третья попытка
Если отличие от рабочего напряжения от допускаемого больше 3…5%, то выполняется третья попытка  .
.


