Примеры решения задач
Пример 1. Автомобиль движется по шоссе, имеющему радиус кривизны 50 м. Закон движения автомобиля определяется уравнением S =10 + 10t – 0.5t2. Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорение в момент времени t = 5 c. Решение. Найдем общее выражение для скорости автомобиля. Известно, что
Взяв производную по времени от заданного уравнения пути, получим
Значение скорости в данный момент можно найти, если в полученную общую формулу скорости вместо времени подставить заданное значение:
Найдем общее выражение для тангенциального ускорения. Из теории известно, что
Взяв производную по времени от общего уравнения скорости, находим
Значение нормального ускорения найдем, подставив в общее уравнение его известные значения скорости и радиуса кривизны траектории:
Полное ускорение будет геометрической суммой взаимно перпендикулярных тангенциального и нормального ускорений:
Пример 2. Пуля выпущена со скоростью 800 м/с под углом 30° к горизонту. Найти: а) время полета пули до падения на землю; б) скорость полета пули в верхней точке ее траектории; в) дальность полета; г) наибольшую высоту подъема пули; д) радиус кривизны траектории в ее верхней точке. Сопротивлением воздуха пренебречь.
Решение. а) Скорость пули Vo, направленную под углом к горизонту, разлагаем на две составляющие: горизонтальную Vox = Vo cos α = 800 cos 300 = 694 м/с, вертикальную Voy= Vo sin α = 800 sin 300 = 400 м/с. Движение пули можно представить как совокупность двух движений: равномерного, происходящего в горизонтальном направлении по инерции с постоянной скоростью Vox = 694 м/с, и равнопеременного, происходящего в вертикальном направлении под действием силы тяжести со скоростью Vy. При полете пули вверх скорость ее под влиянием силы тяжести будет постепенно уменьшаться по закону Vy = Voy – gt. В верхней точке траектории эта вертикальная скорость будет равна нулю. Следовательно, формула примет вид 0 = Voy – gt. Отсюда находим время полета пули вверх как t = Voy / g= 400 / 9.81 = 40.7 c. Столько же времени будет продолжаться падение пули на поверхность Земли. Следовательно, полная продолжительность полета пули 2t = 2 · 40.7 = 81.4 c. б) В верхней точке траектории результирующая скорость полета пули равна скорости ее в горизонтальном направлении, так как в этой точке вертикальная скорость равна нулю. Следовательно, V = Vx = V0x = 694 м/с. в) В горизонтальном направлении пуля летит с постоянной скоростью Vx = V0 · cos α = 694 м/с. За время полета пуля пройдет расстояние Sx = Vx·2t = 694 · 81.4 = 5.65·104 м. г) За время подъема, равное 40.7 с, пуля пройдет в вертикальном направлении расстояние
Это расстояние и определяет высоту верхней точки траектории над поверхностью земли. д) В самой верхней точке траектории ускорение, сообщаемое пуле силой тяжести и направленное вертикально, совпадает по направлению с нормалью к траектории и поэтому является нормальным. Величина его выражается формулой
где R – радиус кривизны траектории в ее верхней точке. Отсюда
Пример 3. Груз массой 45 кг перемещается по горизонтальной плоскости под действием силы 294 Н, направленной под углом 30° к горизонту. Коэффициент трения груза о плоскость 0.1. Определить ускорение движения груза.
Запишем для данного тела уравнение второго закона Ньютона в векторной форме:
Выбрав направления осей X и Y и найдя проекции сил на оси, запишем это уравнение в скалярной форме:
Из уравнения (3) находим, что
Тогда Подставим это выражение в (2):
откуда найдем ускорение груза:
Пример 4. Тело массой m, находящееся на вершине наклонной плоскости, удерживается силой трения. За какое время тело спустится с наклонной плоскости, если плоскость станет двигаться в горизонтальном направлении с ускорением a0 = 1 м/с2. Длина плоскости l =1 м, угол наклона к горизонту a =30°, коэффициент трения между телом и плоскостью m = 0.6. Решение. Выберем систему отсчета, связанную с наклонной плоскостью. Пока плоскость покоится, на тело действуют три силы: сила тяжести
Равновесие нарушится, и тело начнет скользить вниз по наклонной плоскости с ускорением
то надо найти ускорение
Проектируя все векторы, входящие в уравнение (2), на оси X и Y, получим два скалярных уравнения: mg sin a – Fтр + ma0 cos a = ma, (3) –mg cos a + N + ma0 sin a = 0. (4) Решив систему уравнений (3), (4) с учетом Fтр = mN, найдем ускорение: а = g (sin a – m cos a) + a0 (cos a +m sin a). Сделаем подстановку в формулу (1):
Подставив числовые значения величин, найдем t = 0.8 c. Пример 5. Молот массой 5 кг, двигаясь со скоростью 4 м/с, ударяет по железному изделию, лежащему на наковальне. Масса наковальни вместе с изделием равна 95 кг. Считая удар абсолютно неупругим, определить энергию, расходуемую на ковку изделия. Чему равен КПД процесса ковки при данных условиях? Решение. Обоснуем возможность применения законов сохранения для решения задачи. Система «молот – изделие – наковальня» не является замкнутой: на нее действуют извне сила тяжести (M + m) g и сила давления N опоры, на которой стоит наковальня. Во время удара молота вторая сила, в той или иной степени определяемая упругими свойствами опоры, будет превышать первую силу и к рассматриваемой системе будет приложена извне равнодействующая R = N – (M + m)g. Однако силы ударного взаимодействия тел весьма велики. Можно предположить, что по сравнению с этими силами величиной R можно пренебречь и, таким образом, считать систему замкнутой. На основании закона сохранения энергии можно утверждать, что энергия, затраченная на деформацию изделия, равна разности значений механической энергии системы до и после удара. Так как во время удара изменяется только кинетическая энергия тел (незначительным перемещением тел по вертикали за время удара мы пренебрегаем), то энергия деформации
где V* – общая скорость всех тел системы после неупругого удара. Ее найдем на основании закона сохранения импульса:
Подставив в формулу (1) значение V* из уравнения (2), получим ответ на первый вопрос задачи:
Так как энергия, расходуемая на ковку изделия, по замыслу задачи является полезной, то КПД процесса ковки
Подставив числовые значения заданных величин в формулы (3) и (4) и выполнив вычисление, получим: Wдеф = 38 Дж, η = 0.95.
Пример 6. Человек стоит в центре скамейки Жуковского и вместе с ней вращается по инерции, делая 0.5 об/с. Момент инерции тела человека относительно оси вращения равен 1.6 кг × м2. В вытянутых в стороны руках человек держит две гири массой по 2 кг каждая. Расстояние между гирями 1.6 м. Сколько оборотов в секунду будет делать скамейка с человеком, если он опустит руки и расстояние между гирями станет равным 0.4 м? Моментом инерции скамейки пренебречь. Решение. Человек, держащий гири, составляет вместе со скамейкой изолированную механическую систему, поэтому момент импульса этой системы должен иметь постоянное значение. Следовательно, для нашего случая
где J1 и ω1 – момент инерции тела человека и угловая скорость скамейки и человека с вытянутыми руками; J2 и ω2 – момент инерции тела человека и угловая скорость скамейки и человека с опущенными руками. Отсюда
Заменив в (2) угловую скорость ее выражением через число оборотов в единицу времени (ω = 2 πν;) и сократив на 2 π;, получим
Момент инерции системы, рассматриваемой в данной задаче, равен сумме момента инерции тела человека J0 и момента инерции гирь в руках человека. Так как размер гирь много меньше расстояния их от оси вращения, то момент инерции гирь можно определить по формуле момента инерции материальной точки
Следовательно,
где m – масса каждой из гирь; l1 – первоначальное расстояние между гирями; l2 – конечное расстояние между гирями. Подставляя выражения J1 и J2 в (3), получим
Подставляя числовые значения в (4), получим
Пример 7. Маховик имеет вид диска массой 50 кг и радиусом 20 см. Он был раскручен до скорости вращения 480 об/мин и затем предоставлен самому себе. Под влиянием трения маховик остановился. Найти момент силы трения, считая его постоянным, если маховик до полной остановки сделал 200 оборотов. Решение. Применим формулу, выражающую связь работы с изменением кинетической энергии,
Работа при вращательном движении определяется по формуле A = Mφ. Подставив это выражение работы, а также выражение момента инерции диска в (1), получим
Отсюда момент силы трения
Угол поворота φ = 2πN = 1256 рад. Подставив числовые значения в (2), найдем момент силы трения: М = – 1 H × м. Знак «минус» показывает, что момент силы трения оказывает тормозящее действие.
Пример 8. Материальная точка массой 5 г совершает колебания с частотой 0.5 с–1. Амплитуда колебаний 3 см. Определить: а) скорость точки в момент времени, когда смещение ее равно 1.5 см и положительно; б) максимальную силу, действующую на точку; в) полную энергию колеблющейся точки. Решение. а) Уравнение гармонического колебания имеет вид x = А sin(ωt + φ;), (1) где x – смещение колеблющейся точки от положения равновесия; А – амплитуда; (ωt + φ;) – фаза колебания; ω; – круговая частота; t – время; φ; – начальная фаза. Формулу скорости получим, взяв первую производную по времени от смещения:
Чтобы выразить скорость через смещение, надо исключить из (1) и (2) время. Для этого возведем оба уравнения в квадрат, разделим первое на А2, второе – на А2ω2 и сложим
или
Решив последнее уравнение относительно V, найдем
Подставив в это выражение числовые значения величин в системе СИ, получим
Знак «плюс» соответствует случаю, когда точка удаляется от положения равновесия (направления смещения и скорости совпадают), знак «минус» соответствует движению точки к положению равновесия (направления смещения и скорости противоположны). Скорость гармонического колебательного движения можно определить также из уравнения x = A cos(ωt +φ;). (4) Взяв вместо (1) уравнение (4) и повторив с ним такое же решение, получим тот же ответ. б) Силу, действующую на точку, найдем по второму закону Ньютона: F = ma, (5) где а – ускорение точки, которое получим, если возьмем производную по времени от скорости,
или
Подставив выражение для ускорения в (5), будем иметь
Отсюда получим максимальное значение силы
Подставив в это уравнение числовые значения величин в системе СИ, найдем
в) Полная энергия колеблющейся точки есть сумма кинетической и потенциальной энергий, вычисленных для любого момента времени. Проще всего вычислить полную энергию в момент, когда кинетическая энергия достигнет максимального значения. В это время потенциальная энергия равна нулю. Поэтому полная энергия Е колеблющейся точки равна максимальной кинетической энергии Wmах и может быть определена по формуле
Максимальную скорость можно определить из формулы (2), если принять cos (ωt + φ;) = 1: Vmax = 2πνA. Подставив это выражение скорости в (6), найдем Е = 2π2mν2А2. После подстановки числовых значений получим
|

 .
. .
. м/с.
м/с. .
. м/с2.
м/с2. м/с2.
м/с2. м/с2.
м/с2.
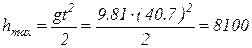 м.
м.
 м.
м. Решение. На груз действуют:
Решение. На груз действуют:  – сила тяжести;
– сила тяжести;  – сила нормальной реакции плоскости;
– сила нормальной реакции плоскости;  – сила тяги и
– сила тяги и  – сила трения.
– сила трения. . (1)
. (1) (2)
(2) (3)
(3)
 .
. ,
, м/с2.
м/с2. , сила нормального давления
, сила нормального давления 
 .
. . Так как искомое время определяется известной формулой пути равноускоренного движения без начальной скорости
. Так как искомое время определяется известной формулой пути равноускоренного движения без начальной скорости (1)
(1) =
= 
 (1)
(1) . (2)
. (2) . (3)
. (3) . (4)
. (4)
 , (1)
, (1) (2)
(2) (3)
(3)


 (4)
(4) об/с.
об/с.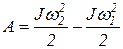 или
или  , (1)
, (1)
 . (2)
. (2) (2)
(2)

 (3)
(3) м/с.
м/с.



 Н.
Н. (6)
(6) Дж.
Дж.


