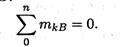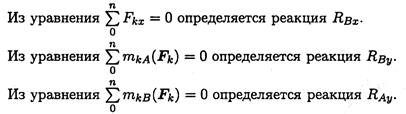Виды нагрузок и разновидности опор

Виды нагрузок

 

По способу приложения нагрузки делятся на

· сосредоточенные и

· распределенные.

Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосре­доточенной.

Часто нагрузка распределена по значительной площадке или ли­нии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают распределенной.

В задачах статики для абсолютно твердых тел распределен­ную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 6.1).

q — интенсивность на­грузки; I — длина стержня;

G = ql — равнодей­ствующая распределенной нагрузки.

Разновидности опор балочных систем (см. лекцию 1)

Балка — конструктивная деталь в виде прямого бруса, закреп­ленная на опорах и изгибаемая приложенными к ней силами.

Высота сечения балки незначительна по сравнению с длиной.

 

Жесткая заделка (защемление) (рис. 6.2)

 

Опора не допускает перемещений и поворотов. Заделку заменя­ют двумя составляющими силы Rax и и парой с моментом Mr.

Для определения этих неизвестных удобно использовать систему уравнений в виде

Каждое уравнение имеет одну неиз­вестную величину и решается без подста­новок.

Для контроля правильности решений используют дополни­тельное уравнение моментов относительно любой точки на балке, например

 

Шарнирно-подвижная опора (рис. 6.3)

Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности.

Шарнирно-неподвижная опора (рис. 6.4)

 

Опора допускает поворот вокруг шарнира и может быть заме­нена двумя составляющими силы вдоль осей координат.

 

Балка на двух шарнирных опорах (рис. 6.5)

Не известны три силы, две из них — вертикальные, следовательно, удобнее для определения неизвестных использовать систему уравнений во второй форме:

 

Составляются уравнения моментов относительно точек крепле­ния балки. Поскольку момент силы, проходящей через точку креп­ления, равен 0, в уравнении останется одна неизвестная сила.

Для контроля правильности решения используется дополни­тельное уравнение

 

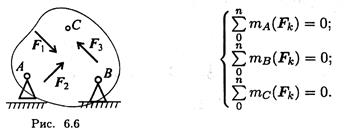
При равновесии твердого тела, где можно выбрать три точки, не лежащие на одной прямой, удобно использовать систему уравнений в третьей форме (рис. 6.6):