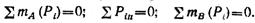Решение. Рассмотрим равновесие балки АВ, к которой приложены как заданные, так и искомые силы
Выбираем систему координат (см. рис. 1.14,6). Составляем три уравненияравновесия:
Решая второе и третье уравнения, получаем:
Составим проверочное уравнение следовательно, опорные реакции определены верно.
Пример 7. Для заданной балки (рис. 1.15, а) определить опорные реакции.
Рассмотрим равновесие балки АВ, к которой приложены все заданные и искомые силы. Освободим балку от связей и заменим их действие реакциями (рис. 1.15, б). Получили плоскую систему произвольно расположенных сил. Выбираем систему координат (см. рис. 1.15, 6). Для полученной системы сил в рассматриваемом примере целесообразно составить следующие три уравнения равновесия:
В этом случае в каждое уравнение равновесия войдет только одна искомая реакция:
где l cos α; — плечо силы RB относительно точки А. Подставляя числовые значения, находим
При определении опорных реакций не было использовано уравнение равновесия ΣPiv = 0. Если реакции определены верно, то сумма проекций на ось v всех сил, действующих на балку, должна быть равна нулю. Проектируя все силы на ось v, получаем
следовательно, реакции определены верно.
Пример 8. Для плоской рамы (рис. 1.16,а) определить опорные реакции.
|
Рассмотрим равновесие балки АВ, к которой приложены как заданные, так и искомые силы. Освобождаем балку от связей и заменяем их действие реакциями (рис. 1.14,6). Получили плоскую систему сил.
Решение
