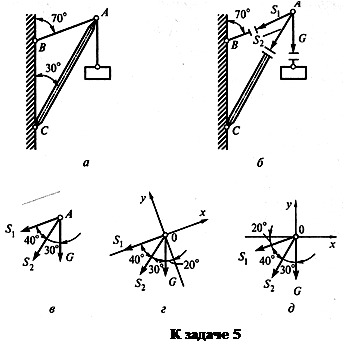
Решение. 1. Рассмотрим равновесие точки А (или узла А), в которой сходятся все стержни и нити.1. 2. Активной силой является вес груза G, направленный вниз (рис. б). 3. Отбросим связи: стержень и нить. Усилие в нити обозначим Sx и направим от точки А, так как нить может испытывать только растяжение. Усилие в стержне обозначим S2 и тоже направим от точки А, предполагая что стержень АС растянут (рис. б). Выполним на отдельном чертеже схему действия сил в точке А (рис. в). 4. Выберем положение системы координат. Начало координат совмещаем с точкой А (рис. г). Ось х совмещаем с линией действия усилия S, а ось у располагаем перпендикулярно оси х. Укажем углы между осями координат и усилиями S1. и S2. 5. Составим уравнения равновесия.
Из второго уравнения находим
Из первого уравнения находим
Знак «минус» перед S2 свидетельствует о том, что стержень АС не растянут, как предполагалось, а сжат.
6. Проверку решения предлагаем выполнить самостоятельно, расположив оси координат так, как показано на рис. д. Ответ: S1 = 15,56 кН, S2 = - 29,24 кН (при принятом на чертеже направлении усилий). Величина усилий зависит от углов наклона стержня и нити. Например, если на рис. а угол 70° заменить на 60°, сохранив угол 30°, то усилия будут равны: S1 = 20 кН, S2 = - 34,64 кН. А при угле 50° S1 = 29,26 кН, S2 = - 44,8 кН. Оба усилия растут и становятся больше веса груза. Пример 6. Как изменятся усилия в стержне и нити, если груз будет перекинут через блок, как показано на рис. а? Остальные данные — в примере 5.
1. Рассматриваемой тонкой остается точка А. 2. Активная сила (вес груза G) действует на точку горизонтально слева направо, так как груз перекинут через блок. 3. Усилия S1 и S2 прикладываем к точке А, как в примере 2. 4. Выбираем систему координат, как показано на рис. б.
5. Составляем и решаем уравнения равновесия:
Из первого уравнения находим
Из второго уравнения находим
Пример 7. Определить усилия в стержнях (рис. а). Массой стержней пренебречь.
|
Рассмотрим равновесие точки А (или узла А), в которой сходятся все стержни и нити.
Решение
Ответ: S1 = 26,94 кН; S2 = - 10,64 кН при принятом направлении усилий на чертеже. Усилие S1 увеличилось, S2 — уменьшилось, а знаки не изменились.
