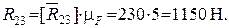С учетом рекомендаций в параграфе 3.1 массы звеньев:
 ,
,
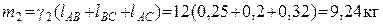 ,
,
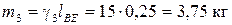 ,
,
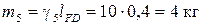 .
.
Силы тяжести звеньев
 ,
,
тогда  ,
,  ,
, 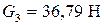 ,
,  .
.
Моменты инерции звеньев
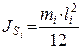 ,
,
 ,
,
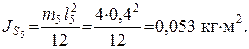
Момент инерции треугольного звена определим, используя выражение (3.21):
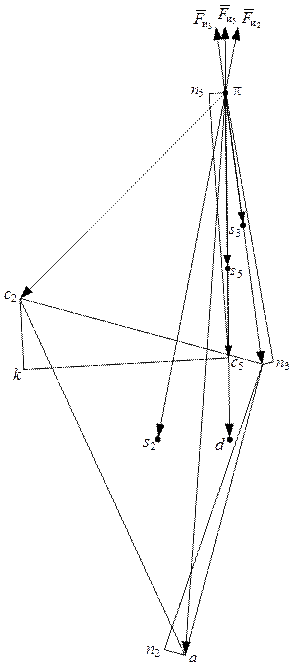 Рис. 3.17 Рис. 3.17
| Для определения сил инерции ускорения, полученные графическим методом в параграфе 2.4.3, сведем в табл. 3.5.
Таблица 3.5
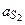
| 
| 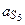
| 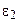
| 
| 
| | м/с2
| с−2
| | 42,5
| 16,25
| 21,15
|
| 1,6
| 105,8
|
Модули сил инерции
 , ,
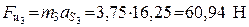 , ,
 . .
Моменты сил инерции:
 , ,
 , ,
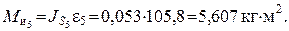
Направления сил инерции определены по плану ускорений, приведенному на рис. 3.17.
Построение плана ускорений рассмотрено в п. 2.4.3.
Силы инерции направим противоположно соответствующим
|
ускорениям центров тяжести звеньев. Моменты сил инерции направим противоположно угловым ускорениям.
3.6.2 Силовой расчет группы звеньев 4 − 5.
Отделим от механизма группу звеньев 4 − 5, разорвав связи звена 5 в шарнире F со стойкой, а связи звена 4 в шарнире  со звеном 2 (рис. 3.18).
со звеном 2 (рис. 3.18).
Действие стойки на звено 5 заменим силой реакции  , которую разложим на две составляющие нормальную
, которую разложим на две составляющие нормальную  (направим вдоль звена FD) и касательную
(направим вдоль звена FD) и касательную  (направим перпендикулярно FD).
(направим перпендикулярно FD).

Рис. 3.19
Действие звена 2 на звено 4 заменим силой  , которая вследствие отсутствия массы ползуна (этой массой пренебрегаем по условию) будет направлена противоположно силе
, которая вследствие отсутствия массы ползуна (этой массой пренебрегаем по условию) будет направлена противоположно силе  (сила действия звена 5 на звено 4).
(сила действия звена 5 на звено 4).
Значит, силу  направим перпендикулярно FD, так как сила
направим перпендикулярно FD, так как сила  в поступательной паре 4 − 5, если пренебречь силами трения, направлена перпендикулярно оси направляющей ползуна (перпендикулярно FD).
в поступательной паре 4 − 5, если пренебречь силами трения, направлена перпендикулярно оси направляющей ползуна (перпендикулярно FD).
Таким образом, имеем три неизвестные величины сил  ,
,  ,
,  , направление которых известно. Для определения силы
, направление которых известно. Для определения силы 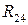 запишем уравнение суммы моментов всех сил относительно точки
запишем уравнение суммы моментов всех сил относительно точки  (
( ):
):
 ,
,
отсюда
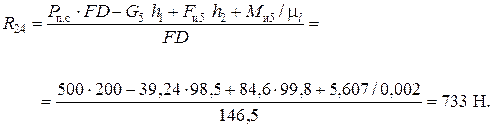
Для определения силы  запишем векторное уравнение суммы сил, действующих на звенья 4 и 5 (
запишем векторное уравнение суммы сил, действующих на звенья 4 и 5 ( ):
):
 .
.
 Рис. 3.19
Рис. 3.19
| Решим это уравнение графически, для чего зададим масштабный коэффициент  .
Разделим величины сил на этот масштабный коэффициент и полученные длины векторов запишем в табл. 3.6.
Таблица 3.6 .
Разделим величины сил на этот масштабный коэффициент и полученные длины векторов запишем в табл. 3.6.
Таблица 3.6
| Сила
| 
| 
| 
| 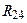
| | Действительная
величина, Н
|
| 84,6
| 39,24
|
| | Масштабная
величина, мм
|
| 16,9
| 7,8
| 146,6
|
Построим план сил. Из намеченной точки отложим по порядку с соответствующими направлениями векторы, изображающие силы в масштабе: 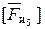 , ,  , ,  , ,  (рис. 3.19). (рис. 3.19).
Для того чтобы замкнуть многоугольник сил, соединим начальную точку с концом последнего отложенного вектора  . Полученный отрезок изобразит силу . Полученный отрезок изобразит силу  . Направим вектор по обходу контура. Модуль силы . Направим вектор по обходу контура. Модуль силы  определим по формуле определим по формуле
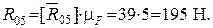
|
3.6.3. Силовой расчет группы звеньев 2 − 3
Отделим от механизма группу звеньев 2 − 3, разорвав связи звена 3 в шарнире Е со стойкой, а связи звена 2 в шарнире А со звеном 1 (рис. 3.20).
Действие стойки на звено 3 заменим силой реакции  , которую разложим на две составляющие: нормальную
, которую разложим на две составляющие: нормальную 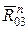 (направим вдоль звена ВЕ) и касательную
(направим вдоль звена ВЕ) и касательную  (направим перпендикулярно ВЕ). Действие звена 1 на звено 2 заменим силой
(направим перпендикулярно ВЕ). Действие звена 1 на звено 2 заменим силой 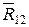 , которую также разложим на две составляющие: нормальную
, которую также разложим на две составляющие: нормальную  (направим вдоль АВ) и касательную
(направим вдоль АВ) и касательную 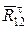 (направим перпендикулярно АВ). Действие звена 4 на звено 2 заменим реакцией связи
(направим перпендикулярно АВ). Действие звена 4 на звено 2 заменим реакцией связи  , которая равна по модулю и противоположна по направлению силе
, которая равна по модулю и противоположна по направлению силе  .
.
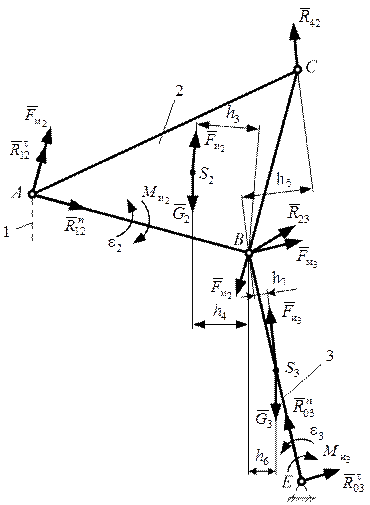
Рис. 3.20
Таким образом, мы имеем четыре неизвестные величины сил 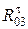 ,
, 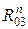 ,
, 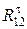 ,
,  направление которых известно. Для определения силы
направление которых известно. Для определения силы 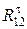 запишем уравнение суммы моментов сил, действующих на звено 2, относительно точки В (
запишем уравнение суммы моментов сил, действующих на звено 2, относительно точки В ( ):
):
 ,
,
отсюда получим:
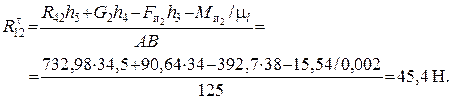
Для определения силы 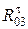 запишем уравнение суммы моментов сил, действующих на звено 3, относительно точки В (
запишем уравнение суммы моментов сил, действующих на звено 3, относительно точки В ( ):
):
 ,
,
отсюда получим:
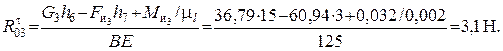
Для определения сил 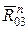 и
и  , а в итоге и полных сил
, а в итоге и полных сил  и
и 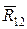 запишем векторное уравнение суммы сил, действующих на звенья 2 и 3 (
запишем векторное уравнение суммы сил, действующих на звенья 2 и 3 ( ):
):
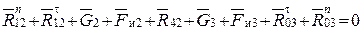 .
.
Решим это уравнение графически, для чего зададим масштабный коэффициент 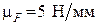 . Разделим величины сил на этот масштабный коэффициент и полученные длины векторов запишем в табл. 3.7.
. Разделим величины сил на этот масштабный коэффициент и полученные длины векторов запишем в табл. 3.7.
Таблица 3.7
| Силы
| 
| 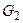
| 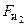
| 
| 
| 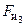
| 
|
| Действительная величина, Н
| 45,4
| 90,64
| 392,7
|
| 36,79
| 60,94
| 3,1
|
| Масштабная величина, мм
| 9,1
| 18,1
| 78,5
| 146,6
| 7,4
| 12,2
| 0,6
|
Построим план сил. Из намеченной точки отложим по порядку с соответствующими направлениями векторы, изображающие силы в масштабе,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  (рис. 3.21). Для того чтобы замкнуть многоугольник сил, через начало вектора
(рис. 3.21). Для того чтобы замкнуть многоугольник сил, через начало вектора  проведем линию, параллельную направлению силы
проведем линию, параллельную направлению силы  (параллельно АВ), а через конец вектора
(параллельно АВ), а через конец вектора  проведем линию, параллельную направлению силы
проведем линию, параллельную направлению силы  (параллельно ВЕ). В результате пересечения этих линий получим отрезки, изображающие силы
(параллельно ВЕ). В результате пересечения этих линий получим отрезки, изображающие силы  и
и 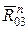 . Направим векторы сил по обходу контура.
. Направим векторы сил по обходу контура.
В результате сложения нормальных и касательных составляющих получим полные силы 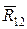 и
и  . Модули этих сил определим по формулам:
. Модули этих сил определим по формулам:
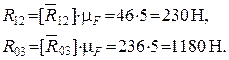

Рис. 3.22
Для определения силы, действующей со стороны звена 2 на звено 3, т. е. реакции связи  (
( ), запишем векторное уравнение суммы сил, действующих на звено 3 (
), запишем векторное уравнение суммы сил, действующих на звено 3 ( ):
):
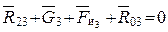 .
.
Соединим начало вектора  с концом вектора
с концом вектора 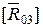 . Полученный отрезок изобразит силу
. Полученный отрезок изобразит силу  в масштабе:
в масштабе:
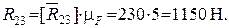

 ,
,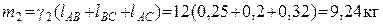 ,
,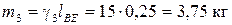 ,
,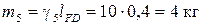 .
. ,
, ,
,  ,
, 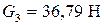 ,
,  .
.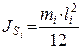 ,
, ,
,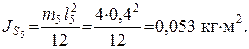
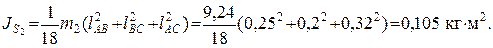
 Рис. 3.17
Рис. 3.17

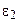


 ,
,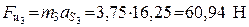 ,
, .
. ,
, ,
,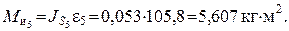
 со звеном 2 (рис. 3.18).
со звеном 2 (рис. 3.18). , которую разложим на две составляющие нормальную
, которую разложим на две составляющие нормальную  (направим вдоль звена FD) и касательную
(направим вдоль звена FD) и касательную  (направим перпендикулярно FD).
(направим перпендикулярно FD).
 , которая вследствие отсутствия массы ползуна (этой массой пренебрегаем по условию) будет направлена противоположно силе
, которая вследствие отсутствия массы ползуна (этой массой пренебрегаем по условию) будет направлена противоположно силе  (сила действия звена 5 на звено 4).
(сила действия звена 5 на звено 4). в поступательной паре 4 − 5, если пренебречь силами трения, направлена перпендикулярно оси направляющей ползуна (перпендикулярно FD).
в поступательной паре 4 − 5, если пренебречь силами трения, направлена перпендикулярно оси направляющей ползуна (перпендикулярно FD). ,
,  ,
,  , направление которых известно. Для определения силы
, направление которых известно. Для определения силы 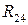 запишем уравнение суммы моментов всех сил относительно точки
запишем уравнение суммы моментов всех сил относительно точки  (
(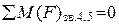 ):
): ,
,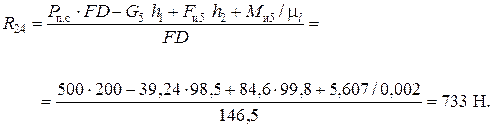
 запишем векторное уравнение суммы сил, действующих на звенья 4 и 5 (
запишем векторное уравнение суммы сил, действующих на звенья 4 и 5 (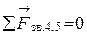 ):
): .
. Рис. 3.19
Рис. 3.19
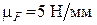 .
Разделим величины сил на этот масштабный коэффициент и полученные длины векторов запишем в табл. 3.6.
Таблица 3.6
.
Разделим величины сил на этот масштабный коэффициент и полученные длины векторов запишем в табл. 3.6.
Таблица 3.6

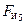

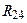
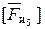 ,
,  ,
,  ,
,  (рис. 3.19).
(рис. 3.19).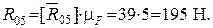
 , которую разложим на две составляющие: нормальную
, которую разложим на две составляющие: нормальную 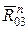 (направим вдоль звена ВЕ) и касательную
(направим вдоль звена ВЕ) и касательную  (направим перпендикулярно ВЕ). Действие звена 1 на звено 2 заменим силой
(направим перпендикулярно ВЕ). Действие звена 1 на звено 2 заменим силой 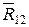 , которую также разложим на две составляющие: нормальную
, которую также разложим на две составляющие: нормальную  (направим вдоль АВ) и касательную
(направим вдоль АВ) и касательную 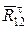 (направим перпендикулярно АВ). Действие звена 4 на звено 2 заменим реакцией связи
(направим перпендикулярно АВ). Действие звена 4 на звено 2 заменим реакцией связи  , которая равна по модулю и противоположна по направлению силе
, которая равна по модулю и противоположна по направлению силе 
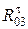 ,
, 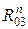 ,
, 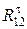 ,
,  направление которых известно. Для определения силы
направление которых известно. Для определения силы  ):
): ,
,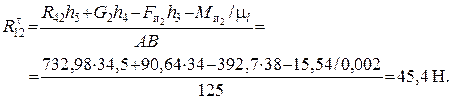
 ):
): ,
,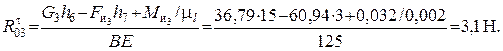
 и
и 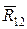 запишем векторное уравнение суммы сил, действующих на звенья 2 и 3 (
запишем векторное уравнение суммы сил, действующих на звенья 2 и 3 ( ):
):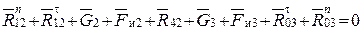 .
. . Разделим величины сил на этот масштабный коэффициент и полученные длины векторов запишем в табл. 3.7.
. Разделим величины сил на этот масштабный коэффициент и полученные длины векторов запишем в табл. 3.7.
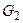
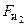


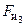

 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  (рис. 3.21). Для того чтобы замкнуть многоугольник сил, через начало вектора
(рис. 3.21). Для того чтобы замкнуть многоугольник сил, через начало вектора  проведем линию, параллельную направлению силы
проведем линию, параллельную направлению силы  проведем линию, параллельную направлению силы
проведем линию, параллельную направлению силы  (параллельно ВЕ). В результате пересечения этих линий получим отрезки, изображающие силы
(параллельно ВЕ). В результате пересечения этих линий получим отрезки, изображающие силы 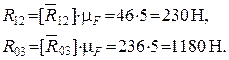

 (
( ), запишем векторное уравнение суммы сил, действующих на звено 3 (
), запишем векторное уравнение суммы сил, действующих на звено 3 ( ):
):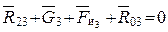 .
. с концом вектора
с концом вектора 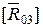 . Полученный отрезок изобразит силу
. Полученный отрезок изобразит силу