Определение масс и моментов инерции звеньев
Центры тяжести стержневых звеньев располагают на осях вращения этих звеньев или в центрах масс фигур. Массы и моменты инерции определяют по эмпирическим формулам. Массы звеньев, имеющих линейные размеры, определяют по формуле
где Если удельный вес Удельные массы Масса поршней в двигателях и компрессорах
где Масса камня кулисы
где Масса долбяков, резцовых призм поперечно-строгальных станков, главных ползунов прессов
где Масса зубчатых колес
где Момент инерции тонкого однородного стержня относительно оси, перпендикулярной стержню и расположенной у одного из его концов (рис. 3.8), определяется по формуле
Момент инерции этого же стержня относительно оси, проходящей через середину стержня (рис. 3.9), определяется по формуле
Этот момент инерции называют центральным, так как он является моментом инерции относительно оси, проходящей через центр тяжести. Рассмотрим звено − «уголок» (рис. 3.10), состоящее из двух жестко соединенных частей
Рассмотрим звено − «уголок» (рис. 3.10), состоящее из двух жестко соединенных частей а) определить момент инерции каждой отдельной части относительно собственного центра масс:
где б) найти положение общего центра масс, используя отношение
в) определить момент инерции всего звена относительно центра масс
Один из авторов данного пособия (О. В. Конищева) предлагает следующий вывод для определения момента инерции «уголка». Заменим отношение (3.14) другим:
где Отсюда
Обозначим
Таким образом, зная геометрические параметры «уголка» можно определить его момент инерции:
Рассмотрим треугольное звено. Здесь могут быть два случая. Первый случай – треугольник представляет собой стержневую конструкцию, приведенную на рис. 3.11, тогда её центр тяжести расположен в центре окружности, вписанной в треугольник, соединяющий середины сторон
Рис. 3.11
На рис. 3.11, точка S – центр вписанной в
Один из авторов пособия (О.В. Конищева) предлагает следующий вывод для определения момента инерции такого треугольного звена. Рассмотрим
Решим эту систему уравнений. Получим
Выразим квадраты этих отрезков, используя тригонометрические формулы:
аналогично
Подставим полученные формулы в выражение (3.17), выразив массы через удельную массу
Таким образом, момент инерции треугольного звена, представляющего собой стержневую конструкцию, определим по формуле
Во втором случае, когда треугольное звено представляет собой пластину, его центр тяжести лежит на пересечении медиан (рис. 3.12). Определим момент инерции «стержневого» треугольника относительно точки, лежащей на пересечении медиан.
Рис. 3.13
В этом случае момент инерции треугольного звена определяется по формуле, аналогичной формуле (3.17):
Один из авторов учебного пособия (О.В. Конищева) предлагает следующий вывод для определения этого момента инерции. Выразим отрезки:
Медианы определяются следующим образом:
Подставим эти выражения в (3.20):
где Таким образом, момент инерции стержневого треугольного звена относительно точки, лежащей на пересечении медиан, определяется по формуле:
Расхождение результатов, полученных по формулам (3.19) и (3.21) составляет 0,75 %, что незначительно. Поэтому, с целью упрощения расчетов стержневого треугольного звена, его центр масс возьмем на пересечении медиан, как для пластины, и момент инерции будем определять по формуле (3.21).
3.6. Силовое исследование шарнирного Построить план механизма в заданном положении, план скоростей и план ускорений для этого положения (эти построения рассмотрены в параграфе 2.4.2 − 2.4.3).
|

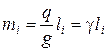 , (3.11)
, (3.11) – масса
– масса  -го звена, кг;
-го звена, кг; 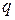 – удельный вес погонного метра звена, Н/м;
– удельный вес погонного метра звена, Н/м;  – ускорение свободного падения,
– ускорение свободного падения,  – длина
– длина 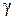 – удельная масса, кг/м.
– удельная масса, кг/м. для шатуна,
для шатуна, 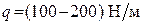 для коромысел,
для коромысел,  для кулис и кривошипов.
для кулис и кривошипов. взять равными
взять равными  .
. ,
,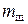 – масса шатуна.
– масса шатуна. ,
, – масса кулисы.
– масса кулисы. ,
, – ход ползуна,
– ход ползуна,  (расстояние между двумя крайними положениями ползуна).
(расстояние между двумя крайними положениями ползуна). ,
, – радиус делительной окружности,
– радиус делительной окружности,  – масса зубчатого колеса.
– масса зубчатого колеса. . (3.12)
. (3.12)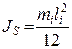 . (3.13)
. (3.13) и
и 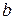 .
. Рис. 3.8
Рис. 3.8
 Рис. 3.9
Рис. 3.9
 Рис. 3.10
Рис. 3.10
 ,
,  ,
, и
и  – массы отдельных частей;
– массы отдельных частей;  ; (3.14)
; (3.14) по формуле
по формуле . (3.15)
. (3.15)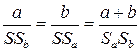 ,
, – отрезок, соединяющий середины отрезков AC и BC, поэтому в треугольнике ABC является средней линией, а значит
– отрезок, соединяющий середины отрезков AC и BC, поэтому в треугольнике ABC является средней линией, а значит  (c = AB).
(c = AB).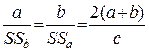 ,
,  ,
,  .
. , тогда выражение (3.15) приобретет вид
, тогда выражение (3.15) приобретет вид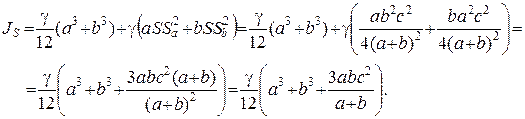
 . (3.16)
. (3.16) .
.
 – середины сторон. Обозначим длины сторон
– середины сторон. Обозначим длины сторон 

 Известно, что момент инерции этого звена определяется по формуле
Известно, что момент инерции этого звена определяется по формуле . (3.17)
. (3.17) . Он подобен
. Он подобен 

 . Выразим длины сторон:
. Выразим длины сторон: (3.18)
(3.18) ,
,  ,
,  .
.
 ,
,  .
.
 . (3.19)
. (3.19)
 . (3.20)
. (3.20) ,
,  ,
,  .
. ,
,  ,
,  .
.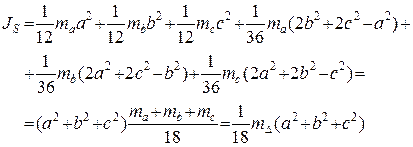
 – масса треугольного звена.
– масса треугольного звена. . (3.21)
. (3.21)


