Виды средних величин и методы их расчета
При анализе статистич. инф-и, хар. различные аспекты развития внеш торговли, важное место занимают средние стат показатели. Средняя величина - один из распр. способов обобщений колич. показателей. Это показатель, хар. качественно однородную сов-ть исслед явления внеш торговли и отражающий уровень одного из исслед. признаков. Признак, по кот. находится средняя величина, наз. осредняемым. Виды сред. величин: - Структурные – дает общую хар-ку структуры сов-ти: Мо, Ме. - Суммарная - сглаживает различий в величине признака. Сущ различные средние: - средняя арифметическая; - средняя геометрическая; - средняя гармоническая; - средняя квадратическая. 1) Ср. арифм. - наиб распростр. вид средней. Исп-ся для обобщенной хар-ки абс. величин. - Простая - если каждое значение признака в ряду распред-я встречается по 1 разу, то сумма всех значений, дел. на число этих значений.
x1,x2,…,xn - значения признака (например, цена товара); n - количество значений. - Взвешенная - если одно и то же значение признака встречается неск-ко раз: 2) Ср. гармонич. – для обобщенной хар-ки относит. величин. - Простая - Взвешенная 3) Ср. геометр. - для хар-ки относит. величин. 1) Простая: 2) Взвешенная: 4) Ср. квадратическая – для обобщ. хар-ки абсю величин (ошибок) - Простая - Взвешенная.
|

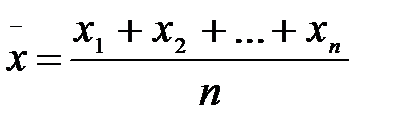
 где xi - значение признака (цена товара), f i - частота повторения этого признака (вес товара).
где xi - значение признака (цена товара), f i - частота повторения этого признака (вес товара).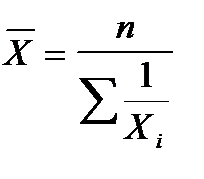
 , где fi – частота признака; xi варианта.
, где fi – частота признака; xi варианта.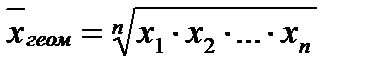 , где x1….xn – значения показателя (н-р, темпа роста).
, где x1….xn – значения показателя (н-р, темпа роста).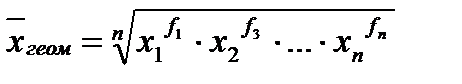 , где x1….xn – значения показателя (н-р, темпа роста), f1…fn - частота признака. В тамож. статистике средняя геометрическая, главным образом, используется для исчисления среднего темпа роста.
, где x1….xn – значения показателя (н-р, темпа роста), f1…fn - частота признака. В тамож. статистике средняя геометрическая, главным образом, используется для исчисления среднего темпа роста.


