Метод аналитического выравнивания. Метод наименьших квадратов. Методология и цели применения.Метод аналитич. выравнивания заключается в выборе адекватной математич. фун-и, кот. наилучшим образом отражает тенденцию развития ряда динамики. Аналитически тренд представляется как функция f(t),зависящая от времени. Реальные данные у называют эмпирическими уровнями ряда динамики. Точки, принадлежащие линии тренда, это значения f(t) для соответствующих значений t. Их называют расчетными значениями, или теоретич/ уровнями ряда динамики. При построении фун-и тренда необходимо решить две задачи: определить класс фун-и для описания зависимости и оценить параметры этой функции. Фун-и: прямая f(t) = a0+ a1t, парабола 2 порядка f(t) = a0+ a1t +a2t2, экспонента f(t) = a 0a1t. Согласно критерию наименьших квадратов параметры модели подбираются таким образом, чтобы сумма квадратов отклонений фактических значений от расчетных была минимальной. Q = S (yt – f(t))2= min. Если в качестве линии тренда выбрана прямая f(t) = a0+ a1t, то критерий наим квадратов можно записать: Q = S (yt – a0- a1t)2= min. Чтобы из этого условия определить числовые значения a0 и a1, следует взять первые частные производные от Q по a0 и a1 и приравнять их нулю, в результате получим систему нормальных уравнений: S уt = a0n+ a1S t, S tyt = a0S t + a1S t2 Центрируя время так, чтобы
|
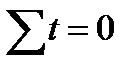, получим формулы для параметров a0 и a1: 
, 
. Аналогично получаются системы уравнений для параболы и экспоненты.
