Абсолютные и относительные величины. Единицы измерения относительных и абсолютных величин.
Статистич. показатели могут быть предс тавлены абсолютными, относительными и средними величинами. Абсолютные показатели являются первичными, а относительные и средние - их производными. 1. Абсолютные показатели выражают размеры, уровни, объемы, имеют натуральное и денежное измерения (измеряются в натуральных единицах измерения - шт, кг, куб. м), Они дел. на: - индивидуальные (вес товара, содержащийся в одной ГТД,) - суммарные (сумма веса товара по всем ГТД) 2. Относительные величины - частное от деления 2 величин и хар-т количественное соотношение между ними. При расчете относитю величин, следует иметь ввиду, что в числителе всегда находится показатель, отражающий явление, кот. надо изучать, т.е. сравниваемый, а в знаменателе - показатель, с кот. производится сравнение (измер. в коэффициентах или %). По своему значению они дел. на: 1) Относит. величины структуры - хар-т состав изучаемых сов-тей (отношение части к целому) (н-р, доля студентов 4.1. на ФТД) 2) Относит. величины сравнения - отражают колич. соотношение одноименных показателей, т.е. показывают во ск-ко раз (или на сколько %) один показатель больше (меньше) другого. 3) Относит. величины динамики – хар-т изменение изучаемого явления во времени (темп роста, темп прироста). (Единств. вид относит величин, кот. имеет ед. измерения, исп. для сравнения разноимен. сов-тей). (на 1 магазин – 100 чел = чел/магазин) 4) Относит. величины интенсивности - показывают, ск-ко единиц одной сов-ти приходится на единицу другой. 5) Относит величины координации – хар-т соотношение между отдельными частями статистич. сов-ти, и показывает во ск-ко раз сравниваемая часть больше или меньше части, кот. принимается за базу сравнения. (студенты и преподаватели – соотн-е).
Средняя величина. Основные понятия, виды средних и методы их расчета. При анализе статистич. инф-и, хар. различные аспекты развития внеш торговли, важное место занимают средние стат показатели. Средняя величина - один из распр. способов обобщений колич. показателей. Это показатель, хар. качественно однородную сов-ть исслед явления внеш торговли и отражающий уровень одного из исслед. признаков. Признак, по кот. находится средняя величина, наз. осредняемым. Виды сред. величин: - Структурные – дает общую хар-ку структуры сов-ти: Мо, Ме. - Суммарная - сглаживает различий в величине признака. Сущ различные средние: - средняя арифметическая; - средняя геометрическая; - средняя гармоническая; - средняя квадратическая. 1) Ср. арифм. - наиб распростр. вид средней. Исп-ся для обобщенной хар-ки абс. величин. - Простая - если каждое значение признака в ряду распред-я встречается по 1 разу, то сумма всех значений, дел. на число этих значений.
x1,x2,…,xn - значения признака (например, цена товара); n - количество значений. - Взвешенная - если одно и то же значение признака встречается неск-ко раз: 2) Ср. гармонич. – для обобщенной хар-ки относит. величин. - Простая - Взвешенная 3) Ср. геометр. - для хар-ки относит. величин. 1) Простая: 2) Взвешенная: 4) Ср. квадратическая – для обобщ. хар-ки абсю величин (ошибок) - Простая - Взвешенная.
|

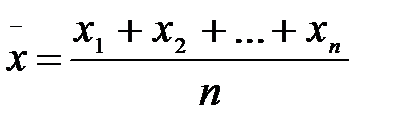
 где xi - значение признака (цена товара), f i - частота повторения этого признака (вес товара).
где xi - значение признака (цена товара), f i - частота повторения этого признака (вес товара).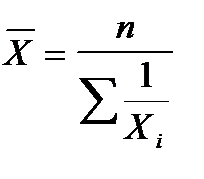
 , где fi – частота признака; xi варианта.
, где fi – частота признака; xi варианта.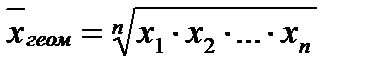 , где x1….xn – значения показателя (н-р, темпа роста).
, где x1….xn – значения показателя (н-р, темпа роста).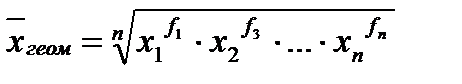 , где x1….xn – значения показателя (н-р, темпа роста), f1…fn - частота признака. В тамож. статистике средняя геометрическая, главным образом, используется для исчисления среднего темпа роста.
, где x1….xn – значения показателя (н-р, темпа роста), f1…fn - частота признака. В тамож. статистике средняя геометрическая, главным образом, используется для исчисления среднего темпа роста.


