Использование показателей вариации для анализа дифференциации цен
Вариация – изменение клич. признака в пространстве. В статистике вариация – это колич. изменения величины исслед. признака в пределах однород. сов-ти, кот. обуслов. влиянием различ. факторов. Она бывает: случайная и систематическая. Виды показателей вариации: - абсолютные (размах вариации (Rв=Xmax-Xmin), среднее абс. линейное отклонение, среднеквадратич. отклонение, дисперсия). - относительные (коэф. вариации, коэф. осцилляции, относит. линейное отклонение). О дифференциации правильнее говорить, когда различия в значениях показателей обусловлены нек. кач-ми отличиями между группами единиц наблюдения. Применительно к анализу цен необх. на 1 этапе исследовать вариацию, с тем чтобы выяснить, какие значения может принимать цена товара, и может ли все многообразие наблюдаемых цен объясняться только случайностью. В том случае, если вариация позволяет предположить неоднородность цен данного товара, следует изучать их дифференциацию, то есть оценивать степень различий, искать их причины и измерять влияние факторных признаков на цену. Для построения вар. рядов распределения исход. инф-ей служат значения конкретных цен опр. товара по каждой записи БД ДТ. Затем записи группируются по значениям средних цен, рассчит. статисчит. хар-ки и строится график. Осн. статистич. хар-ки: различ. виды средних, показатели вариации относительно среднего, а также показатели асимметрии (скошенности) и эксцесса (крутости) распределения. 1. Rb размах вариации: определяет расстояние от min до max значения показателя. «+» просто вычисляется, «-»чувствителен к случайным экстремальным значениям.
2. Cреднее абсолют. линейное отклонение d: более устойчивый показатель вариации. - Простое: - Взвешенное: 3. Дисперсия D: средняя арифм. квадратов отклонений каждого значения признака от общей средней. позволяет раскладывать общую вариацию показателя по факторам, что важно при анализе взаимосвязей. «-» - ее размерность (н-р, дисперсия цены будет измеряться в руб. или долл. в квадрате), что мешает наглядности представления рассеивания относительно среднего. - Простая: - Взвешенная: 4. Среднеквадратичное отклонение σ;:позволяет наглядно представить среднюю ширину распределения в первонач. единицах измерения. - Простое: - Взвешенное - для сгруппированных данных: 5. Относительными показателями вариации являются: - VK = R/xcp х 100 % — коэффициент осцилляции; - Vd = d/xсрх 100 % — относительное линейное отклонение; - К = σ/хср х 100 % — коэффициент вариации. Относительные показатели вариации являются мерой устойчивости значений показателя. Чем они меньше, тем устойчивее ряд и надежнее все выводы и оценки статистического анализа. 6. Для исследования дифференциации особое значение имеют первый (нижний) Q, и последний (верхний) Q;1 квартили, отсекающие 1/ 4 исходной сов-ти соответственно снизу и сверху. При анализе вариации и дифференциации представляет интерес определение значений показателя, делящих всю сов-ть на 4 (квартили), 10 (децили), 100 (перценгили) равных частей, они имеют также общее название — квантили. Коэффициент дифференциации рассчитывают по формуле: 7. Для опр. формы хар-ки распред-я: - Коэф. асимметрии: - Коэф. эксцесса:
|

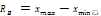 , где хmaх и xmin — макс и мин цена распред-я /
, где хmaх и xmin — макс и мин цена распред-я /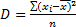
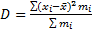
 Или корень из дисперсии:
Или корень из дисперсии: 

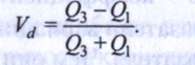 Он хар-т квартильное отклонение в относит. единицах.
Он хар-т квартильное отклонение в относит. единицах.


