Прогнозирование объемов внешней торговли и поступления таможенных платежей в федеральный бюджет. Основные принципы и подходыПрогнозирование объемов таможенных платежей, перечисляемых в Федеральный бюджет РФ, является для современной российской экономики самым серьезным из аспектов при планировании Федерального бюджета на последующие годы. При долгосрочном прогнозировании учитываются тенденции развития мирового хозяйства и состояние экономики нашей страны, которые находят отражение в увеличении или уменьшении товарооборота через таможенную границу России. Важной задачей таможенной статистики является прогнозирование временных рядов (объемов внешней торговли, таможенных платежей и т.д.). Построение прогнозов является самым последним этапом анализа временных рядов. Основными методами выявления тенденции рядов динамики явл.: 1.метод укрупнения интервалов (исходный ряд динамики заменяется более крупными интервалами (месяц на квартал)); 2.метод скользящей средней; 3.метод аналитич. выравнивания. Чаще всего примен-ся 3-й метод. Метод аналитического выравнивания заключается в выборе адекватной математической функции, которая наилучшим образом отражает тенденцию развития ряда динамики. Аналитически тренд представляется как функция f(t),зависящая от времени. Реальные данные у называют эмпирическими уровнями ряда динамики. Точки, принадлежащие линии тренда, это значения f(t) для соответствующих значений t. Их называют расчетными значениями, или теоретическими уровнями ряда динамики. При построении функции тренда необходимо решить две задачи: определить класс фун-и для описания зависимости и оценить параметры этой функции. В качестве модели тренда можно использовать любую подходящую функцию, однако чаще всего используют: прямую f(t) = a0 + a1 t, параболу второго порядка f(t) = a0 + a1 t +a2 t2, экспоненту f(t) = a 0 a1 t. Лин ф-я использ-ся для равномерного развития. Согласно критерию наименьших квадратов параметры модели подбираются таким образом, чтобы сумма квадратов отклонений фактических эмпирич значений от расчетных была минимальной. Q = S (yt – f(t))2= min. Если в качестве линии тренда выбрана прямая f(t) = a0 + a1t, то критерий наименьших квадратов можно записать: Q = S (yt – a0 - a1t)2= min. Чтобы из этого условия определить числовые значения a0 и a1, следует взять первые частные производные от Q по a0 и a1 и приравнять их нулю, в результате получим систему нормальных уравнений: S уt = a0n+ a1S t, S tyt = a0 S t + a1 S t2 Центрируя время так, чтобы Ряды динамики дают картину изменения показателей за прошедшее время, но часто на базе этих показателей требуется получить оценку развития на будущее. Для этого применяется метод экстраполяции. Если же нужно достроить какие-либо значения в прошедшем периоде, то - интерполяция.
|
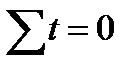, получим формулы для параметров a0 и a1: 
, 
.
