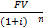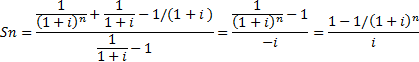Вопрос – изменение стоимости денежных единиц во времени. Операции накопления и дисконтирования.
Одна и та же денежная сумма относящаяся к разным промежуткам времени имеет разную стоимость и ценность. Это объясняется существованием инфляции, ставкой дохода на капитал, инвестиционными рисками(Любое направление инвестирования характеризуется определенными рисками. Безрискового инвестирования нет. Инвестор может потерять денежную сумму, вложенную в проект и не получить доходы, на которые он рассчитывал) и психологические предпочтения людей(Обычно считается что человек выберет определенную денежную сумму сумму сегодня чем точно такую же в будущем. За ожидание человек обычно хочет получить дополнительный доход, который также будет описываться ставкой дохода на капитал). Для управления финансами предприятия необходимо производить операции (Сравнение, сложение, расчет разницы) с денежными суммами которые относятся к разным моментам времени. Так как ценность этих сумм не одинаковая – их нельзя сравнивать, складывать и отнимать без дополнительных операций. Все эти денежные суммы необходимо приводить к одному и тому же моменту времени. Эти действия можно производить с помощью операций накопления и дисконтирования. Накопление – расчет бедующей стоимости известной на настоящий момент денежной суммы. Дисконтирование – операция обратная операции накопления – определение настоящей (текущей, приведенной, сегодняшней) стоимости известной в будущем денежной суммы. В обеих операциях используется процентная ставка, которая в операции накопления называется ставкой дохода на капитал, а в операции дисконтирования – ставка дисконта. 2.Вопрос. Простой и сложный процент. Накопление денежной суммы может происходить по схеме простого и сложного процента. Простой процент- подразумевает что проценты начисляются все время на одну и ту же первоначальную (основную) сумму. При сложном проценте – проценты начисляются на увеличенную за счет начисленных за предыдущие периоды проценты сумму. Накопление по схеме простого и сложного процента Пусть первоначальная сумма равна 1 ден.ед. А процент равен i
FV=(1+i)n – Future value при PV (Present Value) = 1 ден.ед. При PV не равной 1 ден.ед FV=PV*(1+i)n n – количество лет Это функция накопления а функция дисконтирования
3.Вопрос.Более частое накопление. Номинальное, периодическое и эффективная ставка процента. В финансовых отчетах начисление процентов может происходить чаще одного раза в год. При этом необходимо: 1)Рассчитать Периодическую ставку процента
2) Увеличить число периодов начисления процентов(накопления) в m раз. M*n Тогда => FV=PV*(1+1/n)m*n
Эффективная ставка процента – действительная ставка по которой начисляется доход за один год. PV (Текущая стоимость)=1000 FV (Будущая стоимость)=1100 Iэф= Задача: Рассчитать эффективную ставку, если номинальная 12%. Начисление производится 1) 2 раза в год 2) Раз в квартал 3) Каждый месяц 4)Каждый день 1) iэф = 2)iэф= 3)iэф= 4)iэф= !!! Рост ограничен e^(i*n) Правило 72 Выводится на основании натуральных логарифмов. Действует в промежутке 3%-18%. Если вы хотите узнать за сколько лет сумма которую вы положите в банк удвоится необходимо 72/целочисленное значение процентов под которые вы положили деньги в банк. Верно также и обратное. Чтобы рассчитать процент, под которые необходимо положить деньги в банк, чтобы сумма удвоилась за нужное количество лет – нужно 72/ данное количество лет. Текущая стоимость аннуитета Аннуитет – поток из n равных платежей, каждый из которых происходит в конце периодического интервала. Текущая его стоимость – стоимость этого потока платежей на сегодняшний момент времени. Ден.Ед PMT Поток n равных платежей Поток платежей Текущая неизвестная стоимость аннуитета Для вывода формулы расчета ТСА предположим, что PMT=1 ден.ед. Для вывода формулы необходимо: 1)Оценить текущую стоимость каждого платежа отдельно; 2)Найти сумму этих текущих стоимостей. Находим текущую стоимость первого платежа:
Второго
Получаем прогрессию: q=1/(1+i) S=(an*q-a1)/(q-1)
Если платеж не равен единице то An=
|

 где I – ставка дисконта, а n – количество лет
где I – ставка дисконта, а n – количество лет , где i- номинальная ставка, а m- количество периодов начисления процентов в году.
, где i- номинальная ставка, а m- количество периодов начисления процентов в году.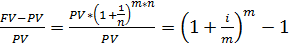


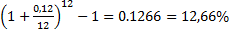


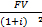 /…/
/…/