Формулы.
(1)
(2)
Билет №20 «Понятие производной функции. Вычисление производной по определению» Определение: предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к 0 называют производной функцией в точке х˳ lim
1) Находим приращение функции на отрезке
Билет №21 «Правила дифференцирования (доказать 1 и 2 правило)» Операция нахождения производной функции называют дифференцированием. 1. Производное суммы (f(x)+g(x))ˡ=fˡ(x)+gˡ(x) Доказательство: n(x)=f(x)+g(x), hˡ(x)-? 1) Х – фиксированная точка ΔХ – приращение аргумента Х+ΔХ – новый аргумент 2) Δy=h(x+Δx)-h(x)=(f(x+Δx)+g(x+Δx))-(f(x)+g(x))=(f(x+Δx)-f(x))+(g(x+Δx)-g(x)) 3) Δx→0 (под каждым lim)
2. Постоянный множитель можно выносить за знак производной (c·f(x))ˡ=c·fˡ(x) Доказательство: h(x)=c·f(x) 1) X – фиксированная точка ΔХ – приращение аргумента Х+ΔХ – новый аргумент Докажем формулу Произвольный множитель можно выносить за знак предельного перехода (это известно из свойств предела), поэтому
3. Производное произведения (f(x)·g(x))ˡ=fˡ(x)·g(x)+f(x)·gˡ(x) 4. Производное частного
5. Производное сложной функции f(g(x))ˡ=fˡ(g(x))·gˡ(x)
Билет №22. Таблица Производных. 1)Степенная функция. а) f(x) = x p , p є R (x p)' = p • x p-1 2) f(х) = а х, а>0, а ≠1 (а х)' = а х • Ln a,( (3 х)’= 3 х • Ln 3 (e х)' = e х , е=2,7 3) Логорифмическая функция. f(x) = ( ( 4)Тригонометрические функции. (sin x)' = cos x (cos x)’= -sin x (tg x)’ = (ctg x)’= Билет №23 Геометрический и физический смысл производной.
|

 = fˡ(x˳)
= fˡ(x˳) :
: 

 устремляя
устремляя  к нулю. Переход к пределу мы будем записывать с помощью знака lim:
к нулю. Переход к пределу мы будем записывать с помощью знака lim:
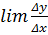 =lim
=lim  =lim
=lim  + lim
+ lim  =fˡx+gˡx
=fˡx+gˡx . По определению производной имеем:
. По определению производной имеем:

 =
= 
 =
=  )
) , а>0, а ≠1
, а>0, а ≠1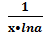

 )' =
)' = 





