Вопрос 33. Формула Ньютона-Лейбница
Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x), вычислить ее значения в точках a и b и найти разность F(b) – F(a).
Вопрос 34.Площадь криволинейной трапеции Криволинейная трапеция - фигура, ограниченная снизу отрезком [a;b] оси Ох, сверху графиком непрерывной функции y=f(x), принимающей положительные значения, а по бокам ограничена отрезками прямых х=а; х=b
35. Геометрический смысл интеграла. Если f (x) непрерывна и положительна на [ a, b ], то интеграл
представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f (x).
Фигура, ограниченная снизу отрезком [ a, b ] оси OX, сверху графиком непрерывной функции, принимающей положительное значение, а по бокам отрезками прямых x = a, x = b – эта фигура называется криволинейной трапецией. Площадь криволинейной трапеции вычисляется по формуле: S=
36. Аксиомы стереометрии и следствия из них. Аксиома – утверждение, не требующее доказательств. Стереометрия - это раздел математики (геометрии), в котором изучаются свойства фигур в пространстве. Аксиома № 1:Через любые 3 точки, не лежащие на одной прямой, проходит плоскость и при том только одна. Аксиома № 2:Если 2 точки прямой лежат в плоскости, то и все точки этой прямой лежат в этой плоскости. Аксиома № 3:Если 2 плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. Следствия из аксиом: 1. Через прямую и не лежащую на ней точку проходи плоскость и при том только одна. 1) Точка В лежит на прямой а, точка С лежит на прямой а; 2) Точки А, В, С лежат в плоскости 3) Точки В, С лежат в плоскости 2. Через 2 пересекающиеся прямые проходит плоскость и при том только одна.
1) Точка В лежит на прямой а, точка С лежит на прямой b; 2) Точки В, А, С лежат в плоскости 3) С лежит в
37. Взаимное расположение прямой и плоскости, двух прямых, двух плоскостей в пространстве. 1. Взаимное расположение прямой и плоскости в пространстве: 1) Прямая лежит в плоскости
2) Прямая и плоскость пересекаются
3) Прямая и плоскость параллельны
2. Взаимное расположение двух прямых в пространстве: 1) Прямые пересекаются (лежат в одной плоскости)
2) Прямые параллельны
3) Скрещивающиеся прямые – две прямые, которые не лежат в одной плоскости
3. Взаимное расположение двух плоскостей в пространстве: 1) Плоскости пересекаются
2) Плоскости параллельны, если они не пересекаются
38. Признак параллельности прямой и плоскости. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна этой плоскости. Дано: а b a II b
Доказать: а II Докажем методом от противного: предположим, что а
39. Признак скрещивающихся прямых. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые являются скрещивающимися. Дано: АВ СD СD C
Доказать: АВ и CD – скрещивающиеся Докажем методом от противного: пусть прямые AB и CD не являются скрещивающимися, тогда они лежат в некоторой плоскости
40. Угол между прямыми в пространстве. 1. Если прямые пересекаются, то углом между прямыми считается меньший из вертикальных углов. 2. Если прямые параллельны или совпадают, то угол между ними равен 0. 3. Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, параллельными данным скрещивающимся.
41. Признак параллельности двух плоскостей. Свойства параллельных плоскостей. Если 2 пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Дано: Плоскости аb а a Доказать: Докажи методом от противного: 1) Предположим, что 2) Прямые а и b лежат в одной плоскости 3) b1 Свойства параллельных плоскостей: 1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
2. Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.
ВОПРОС 42 СЕЧЕНИЯ ТЕТРАЭДРА И ПАРАЛЛЕЛЕПИПЕДА. ПРИНЦИП И СВОЙСТВА ПРАВИЛЬНОГО ПОСТОРОЕНИЯ СЕЧЕНИЙ Тетраэдр (Т) – поверхность, составленная из 4-ех треугольников. Параллелепипед (П) – поверхность, составленная из 2-ух равных параллелограммов, находящихся в параллельных плоскостях, и 4-ех параллелограммов. Плоскость называется секущей плоскостью Т (П), если по обе стороны от этой плоскости имеются точки данного Т (П). Многоугольник, сторонами которого являются отрезки, по которым секущая плоскость пересекает грани Т (П) называется сечением Сечением тетраэдра могут быть трёх- и четырёхугольники, а сечением параллелепипеда – трёх-, четырёх-, пяти-, шестиугольники. Принципы построения сечений. 1. Если известны 2 точки секущей плоскости, принадлежащей одной грани, то надо их соединить. 2. Если известен отрезок, по которому секущая плоскость пересекает грани, то надо продолжить этот отрезок до пересечения с продолжением других ребер этой грани и получить новые точки секущей плоскости. Свойства правильного построения сечения. 1. Все вершины сечения должны лежать на ребрах. 2. Все стороны сечения – в гранях. 3. В каждой грани лежит не более одно стороны сечения. 4. Если секущая плоскость пересекает противоположные грани параллелепипеда по каким-то отрезкам, то эти отрезки параллельны. ВОПРОС 43. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ. Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90 градусам. ü Перпендикулярные прямые могут быть скрещивающимися или пересекающимися. Прямая называется перпендикулярной плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости · Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к плоскости · Если две прямые перпендикулярны к плоскости, то они параллельны
Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости. ВОПРОС 44. РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ. Расстояние от точки до плоскости – это расстояние от данной точки до основания перпендикуляра, проведенного из заданной точки к заданной плоскости. Перпендикуляр, проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из этой же точки к этой плоскости. ВОПРОС 45. ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ.
Доказательство. 1. Рассмотрим плоскость АМН: Прямая а перпендикулярна плоскости АМН, т.к. прямая а перпендикулярна двум пересекающимся прямым АН (прямая а перпендикулярна прямой АН, т.к. прямая АН перпендикулярна плоскости альфа) и НМ (по усл.) 2. Прямая а перпендикулярна плоскости АМН, АМ лежит в плоскости АМН. Из этого следует, что прямая а перпендикулярна прямой АМ. Что и требовалось доказать. ВОПРОС 46. ДВУГРАННЫЙ УГОЛ Двугранный угол — геометрическая фигура, образованная двумя полуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоскостями. Полуплоскости называются гранями двугранного угла, а их общая прямая — ребром. Градусной мерой двугранного угла называется градусная мера его линейного угла. ВОПРОС 47. ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ Определение: две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 90 градусам. Признак перпендикулярности плоскостей. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны. Доказательство
Прямая AD перпендикулярна прямой АС; прямая ВА перпендикулярна плоскости β (по условию). Прямая АС лежит в плоскости β, угол BAD – линейный угол двугранного угла, образованного при пересечении плоскостей α и β. Так как прямая АВ перпендикулярна плоскости β, прямая AD лежит в плоскости β, прямая АВ перпендикулярна прямой AD => угол BAD = 90 градусам, следовательно, плоскости α и β перпендикулярны. ЧТД.
|

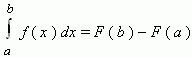












 (по аксиоме 1);
(по аксиоме 1);
 (по аксиоме 1), следовательно а, b лежат в плоскости
(по аксиоме 1), следовательно а, b лежат в плоскости  В лежит в
В лежит в 









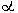

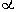

 , следовательно а
, следовательно а 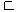
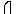
 , но так как b
, но так как b  а, то b
а, то b 
 , что невозможно, так как по условию b
, что невозможно, так как по условию b 
 , ч.т.д.
, ч.т.д.



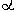

 =C
=C AB
AB . Плоскость
. Плоскость  , следовательно
, следовательно 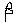 , тогда СD
, тогда СD 
 , что невозможно по условию, значит предположение было не верно, ч.т.д.
, что невозможно по условию, значит предположение было не верно, ч.т.д.

 , a1b1
, a1b1 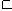

 b=M
b=M 
 a1, b
a1, b 
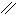



 , тогда
, тогда  пересекает
пересекает  по некоторой прямой С
по некоторой прямой С с прямой c. Согласно теореме о параллельных прямых одна из них может быть параллельна прямой с, а другая например b пересекает прямую с (b
с прямой c. Согласно теореме о параллельных прямых одна из них может быть параллельна прямой с, а другая например b пересекает прямую с (b  c, c
c, c 
 , тогда b
, тогда b 
 )
) b, b
b, b  , тогда b1
, тогда b1 
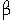 , что невозможно, так как по условиюb1
, что невозможно, так как по условиюb1 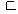
 , следовательно предположение было не верно, ч.т.д.
, следовательно предположение было не верно, ч.т.д.
 Прямая, проведенная к плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, будет перпендикулярна и к самой плоскости.
Прямая, проведенная к плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, будет перпендикулярна и к самой плоскости.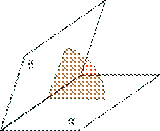
 АС – ребро двугранного угла.
АС – ребро двугранного угла.


