Число строк (столбцов) в определителе называется порядком определителя.
Определители, вообще говоря, могут быть любого порядка. Если все элементы определителя – числа, то определитель также является числом. Для определителей второго и третьего порядков имеют место формулы
Процедура вычисления определителей более высокого порядка будет изложена ниже. Доказано, что свойства определителей не зависят от их порядка, причем свойства, сформулированные для строк справедливы для столбцов. Приведем без доказательства несколько основных свойств определителя. 1) Определители, у которых равны нулю все элементы одной строки или столбца, равны нулю. 2) Если определитель имеет две одинаковых или пропорциональных строки (столбца) он также равен нулю. 3) Если все элементы некоторой строки умножить на любое число и просуммировать их с соответствующими элементами другой строки, значение определителя не изменится. Минором Алгебраическим дополнением . Имеют место формулы, позволяющие вычислить определитель любого порядка. Приведем формулы для определителей третьего и четвертого порядков
здесь
где
Приведенные формулы представляют собой разложение определителей по элементам первой строки. Можно разлагать определитель по элементам любой строки (столбца). Сформулируем еще два свойства определителей. 4) Сумма произведений элементов строки (столбца) на собственные алгебраические дополнения равна значению определителя. 5) Сумма произведений элементов строки на алгебраические дополнения элементов другой строки равна нулю. Примеры. Вычислить определители1) 2) Другой способ (разложение определителя по элементам третьей строки) по формуле (1)
Эти же примеры можно решать с помощью компьютерной системы Maxima. Для этого с помощью команды matrix([15,2],[-7,10]) создадим определитель со строками (15, 2) и (-7,10), затем вычислим этот определитель при помощи команды determinant(matrix([15,2],[-7,10])) и получим ответ 164. Аналогично determinant(matrix([1,2,3],[4,5,6],[7,8,9])) дает ответ 0. §1.2. Метод Крамера решения систем линейных алгебраических уравнений Вернемся к решению системы уравнений
Полученное выше решение
можно записать через определители второго порядка
Эти формулы называют формулами Крамера. Они, кстати, справедливы для систем любого порядка. Определитель, стоящий в знаменателе этих формул, состоит из коэффициентов при неизвестных. Его называют основным определителем системы, поскольку от его значения зависит, совместна ли система уравнений, имеет ли она единственное решение, или их бесчисленное множество. Обозначим его Продолжим анализ полученного решения. Формулы Крамера справедливы при Если Решим этим же методом систему трех уравнений
Как уже говорилось выше, формулы Крамера работают и в этом случае. Пусть основной определитель системы, составленный из коэффициентов при неизвестных, не равен нулю. Итак,
а Пример. Решить методом Крамера систему Основной определитель системы уравнений вычисляем по формуле
Теперь
В соответствии с формулами Крамера (3)
Решим эту же систему также методом Крамера, но с помощью программы Maxima. С помощью команды D: determinant(matrix([1,-2,3],[2,3,-4],[3,-2,-5])) присвоим переменной D значение основного определителя системы, а затем с помощью команд x: determinant(matrix([6,-2,3],[20,3,-4],[6,-2,-5]))/D, y: determinant(matrix([1,6,3],[2,20,-4],[3,6,-5]))/D, z: determinant(matrix([1,-2,6],[2,3,20],[3,-2,6]))/D вычисляем значения неизвестных. Примечание. 1) Метод Крамера применим при решении систем практически любого порядка, если число неизвестных совпадает с числом уравнений и основной определитель системы не равен нулю. 2) В случае §1.3. Матрицы, некоторые их свойства В предыдущем параграфе использовалась функция matrix, с помощью которой вводилась таблица коэффициентов. Такого рода таблицы называют матрицами, и они широко используются в линейной алгебре, да и не только. Матрицы могут быть прямоугольными, когда количество строк и столбцов различное, тогда говорят о матрице размера
|

 ,
, .
. элемента
элемента  определителя называется определитель на единицу меньшего порядка, образованный из исходного определителя вычеркиванием строки и столбца, на пересечении которых расположен данный элемент.
определителя называется определитель на единицу меньшего порядка, образованный из исходного определителя вычеркиванием строки и столбца, на пересечении которых расположен данный элемент. элемента определителя называется выражение, определяемое формулой
элемента определителя называется выражение, определяемое формулой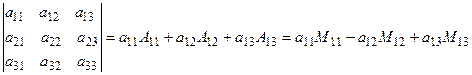 , (1)
, (1)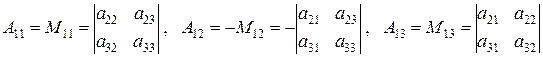 .
. ,
, ,
,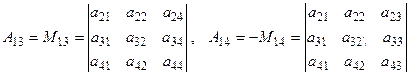 .
. ,
,

 .
.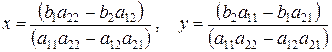
 . (2)
. (2) . Если принять
. Если принять  , то
, то  . Это более привычная запись формул Крамера.
. Это более привычная запись формул Крамера. и дают единственное решение задачи. Вспомним, что они получены из формул
и дают единственное решение задачи. Вспомним, что они получены из формул  , которые можно использовать и при
, которые можно использовать и при  . Если
. Если  , то решений уравнения
, то решений уравнения  , а, следовательно, и системы не существует. Аналогичный результат имеем при
, а, следовательно, и системы не существует. Аналогичный результат имеем при  . Итак, система несовместна, если
. Итак, система несовместна, если 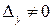 .
. , то оба уравнения превращаются в тождества при любых значениях
, то оба уравнения превращаются в тождества при любых значениях  и
и 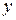 , то есть решений системы бесчисленное множество и определяются они формулой
, то есть решений системы бесчисленное множество и определяются они формулой  при
при  , или
, или  при
при  .
.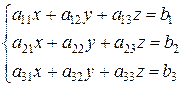 .
. .
. Чтобы получить остальные определители, необходимо подставить столбец свободных членов вместо первого столбца основного определителя, затем вместо второго и третьего. Тогда
Чтобы получить остальные определители, необходимо подставить столбец свободных членов вместо первого столбца основного определителя, затем вместо второго и третьего. Тогда ,
, . (3)
. (3) .
.
 .
.
 . Очевидно, нет смысла вычислять еще один определитель третьего порядка, проще
. Очевидно, нет смысла вычислять еще один определитель третьего порядка, проще 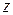 определить с помощью одного из уравнений. Из третьего уравнения следует
определить с помощью одного из уравнений. Из третьего уравнения следует  . Проверим полученный результат, подставив найденные значения неизвестных в первые два уравнения
. Проверим полученный результат, подставив найденные значения неизвестных в первые два уравнения
 , где
, где  число ее строк, а
число ее строк, а  число столбцов. В случае квадратных матриц, у которых число строк и столбцов совпадает, говорят о порядке матрицы. Часто встречаются матрицы -строки и матрицы-столбцы, у первых одна строка, у вторых один столбец.
число столбцов. В случае квадратных матриц, у которых число строк и столбцов совпадает, говорят о порядке матрицы. Часто встречаются матрицы -строки и матрицы-столбцы, у первых одна строка, у вторых один столбец.


