Методы изучения взаимосвязей

Для изучения, измерения и количественного выражения взаимосвязей между явлениями в статистике применяются различные методы, важнейшими из которых являются: метод сопоставления, метод параллельных рядов, балансовый, графический, методы аналитических группировок, дисперсионного и корреляционного анализа.

Метод параллельных рядов. Чтобы установить связь между явлениями, достаточно расположить полученные в результате сводки и обработки материалы в виде параллельных рядов и сопоставить их между собой. Такое сопоставление, проведенное после теоретического анализа, показавшего возможность связи между изучаемыми явлениями, позволяет проследить числовые соотношения сопоставляемых признаков и направление их изменений, т.е. позволяет установить наличие связи и получить представление о ее характере.

Балансовый метод. Для характеристики взаимосвязи между явлениями в статистике применяется балансовый метод. Сущность его заключается в том, что данные взаимосвязанных показателей изображаются в виде таблицы и располагаются таким образом, чтобы итоги между отдельными частями были равны, т.е. чтобы был баланс. Балансовый метод используется для характеристики взаимосвязи между производством и реализацией продукции, денежными доходами и расходами населения и т.д.

Метод аналитических группировок. При наличии массовых статистических данных для изучения массовых явлений широко используются методы аналитических группировок. Аналитические группировки позволяют установить наличие связи между двумя и более признаками и ее направление. Метод группировок сочетается с методом средних и отдельных величин. Сущность метода аналитических группировок заключается в том, что единицы статистической совокупности группируются, как правило, по факторному признаку и для каждой группы исчисляется средняя или относительная величина по результативному признаку. Затем изменения средних или относительных значений результативного признака составляются с изменением факторного признака для выявления характера связи между ними.

Дисперсионный анализ. Аналитические группировки при всей своей значимости не дают количественного выражения тесноты связи между признаками. Эта задача решается при помощи дисперсионного и корреляционного анализов.

Дисперсионной анализ дает прежде всего возможность определить роль систематической и случайной вариации в общей вариации и, следовательно, установить роль изучаемого фактора в изменении результативного признака. Для этого пользуются правилом сложения дисперсий, согласно которому общая дисперсия равна сумме двух дисперсий: средней из внутригрупповых и межгрупповой

Для характеристики тесноты корреляционной связи между признаками в аналитических группировках межгрупповую дисперсию сопоставляют с общей. Это отношение называется корреляционным и обозначается .

Оно характеризует долю вариации результативного признака, вызванного воздействием факторного признака, положенного в основание группировки. Корреляционное отношение по своему абсолютному значению колеблется в пределах от 0 до 1. Чем ближе корреляционное отношение к 1, тем большее влияние оказывает факторный признак на результативный. Если же факторный признак не влияет на результативный, то вариация, обусловленная им, будет равна нулю (δ;² = 0) и корреляционное отношение также равно нулю (η;² = 0), что свидетельствует о полном отсутствии связи. И наоборот, если результативный признак изменяется только под воздействием одного факторного признака, то вариация, обусловленная этим признаком, будет равна общей вариации (δ;² = σ;²), и корреляционное отношение будет равно единице (η;² = 1), что говорит о наличии полной связи.
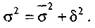
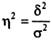