Сущность и виды средних величин
Как правило, многие признаки единиц статистических совокупностей различны по своему значению, например, заработная плата рабочих одной профессии какого-либо предприятия не одинакова за один и тот же период времени, различны урожайность сельскохозяйственных культур в хозяйствах района и цены на рынке на одинаковую продукцию и т.д. Поэтому, чтобы определить значение признака, характерное для всей изучаемой совокупности единиц, прибегают к расчету средних величин. Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину признака в расчете на единицу качественно однородной совокупности по одному варьирующему признаку. В экономической практике используется широкий круг показателей, вычисленных в виде средних величин. Например, обобщающим показателем доходов рабочих акционерного общества (АО) служит средний доход одного рабочего, определяемый отношением фонда заработной платы и выплат социального характера за рассматриваемый период (год, квартал, месяц) к численности рабочих АО. Для лиц с достаточно однородным уровнем доходов, например, работников бюджетной сферы и пенсионеров по старости (исключая имеющих льготы и дополнительные доходы) можно определить типичные доли расходов на покупку предметов питания. Так можно говорить о средней продолжительности рабочего дня, среднем тарифном разряде рабочих, среднем уровне производительности труда и т.д. Вычисление среднего — один из распространенных приемов обобщения; средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимно погашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от количественных значений признака в каждом конкретном случае. В способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних как обобщающих характеристик совокупностей. Там, где возникает потребность обобщения, расчет таких характеристик приводит к замене множества различных индивидуальных значений признака средним показателем, характеризующим всю совокупность явлений, что позволяет выявить закономерности, присущие массовым общественным явлениям, незаметные в единичных явлениях. Средняя отражает характерный, типичный, реальный уровень изучаемых явлений, характеризует эти уровни и их изменения во времени и в пространстве. Средняя — это сводная характеристика закономерностей процесса в тех условиях, в которых он протекает. Анализ средних выявляет, например, закономерности изменения производительности труда, заработной платы рабочих отдельного предприятия на определенном этапе его экономического развития, изменения климата в конкретном пункте земного шара на основе многолетних наблюдений средней температуры воздуха и др. Однако для того, чтобы средний показатель был действительно типизирующим, он должен определяться не для любых совокупностей, а только для совокупностей, состоящих из качественно однородных единиц. Это является основным условием научно обоснованного использования средних. Средние, полученные для неоднородных совокупностей, будут искажать характер изучаемого общественного явления, фальсифицировать его, или будут бессмысленными. Так, если рассчитать средний уровень доходов служащих какого-либо района, то получится фиктивный средний показатель, поскольку для его исчисления использована неоднородная совокупность, включающая в себя служащих предприятий различных типов (государственных, совместных, арендных, акционерных), а также органов государственного управления, сферы науки, культуры, образования и т.п. В таких случаях метод средних используется в сочетании с методом группировок, позволяющим выделить однородные группы, по которым и исчисляются типические групповые средние. Групповые средние позволяют избежать "огульных" средних, обеспечивают сравнение уровней отдельных групп с общим уровнем по совокупности, выявление имеющихся различий и т.д. Однако нельзя сводить роль средних только к характеристике типических значений признаков в однородных по данному признаку совокупностях. На практике современная статистика использует так называемые системные средние, обобщающие неоднородные явления (характеристики государства, единой народнохозяйственной системы: например, средний национальный доход на душу населения, средняя урожайность зерновых по всей стране, средний реальный доход на душу населения, среднее потребление продуктов питания на душу населения, производительность общественного труда). В современных условиях развития рыночных отношений в экономике средние служат инструментом изучения объективных закономерностей социально-экономических явлений. Однако в экономическом анализе нельзя ограничиваться лишь средними показателями, так как за общими благоприятными средними могут скрываться и крупные серьезные недостатки в деятельности отдельных хозяйствующих субъектов, и ростки нового, прогрессивного. Так, например, распределение населения по доходу позволяет выявлять формирование новых социальных групп. Поэтому наряду со средними статистическими данными необходимо учитывать особенности отдельных единиц совокупности. Средняя должна исчисляться для совокупности, состоящей из достаточно большого числа единиц, так как в этом случае согласно закону больших чисел взаимно погашаются случайные, индивидуальные различия между единицами, и они не оказывают существенного влияния на среднее значение, что способствует проявлению основного, существенного, присущего всей массе. Если основываться на среднем из небольшой группы данных, то можно сделать неправильные выводы, поскольку такой средний показатель будет отражать значительное влияние индивидуальных особенностей, т.е. случайных моментов, не характерных для изучаемой совокупности в целом. Каждая средняя характеризует изучаемую совокупность по какому-либо одному признаку, но для характеристики любой совокупности, описания ее типических черт и качественных особенностей нужна система средних показателей. Поэтому в практике отечественной статистики для изучения социально-экономических явлений, как правило, исчисляется система средних показателей. Так, например, показатели средней заработной платы оцениваются совместно с показателями средней выработки, фондовооруженности и энерговооруженности труда, степенью механизации и автоматизации работ и др. Средняя должна вычисляться с учетом экономического содержания исследуемого показателя. Поэтому для конкретного показателя, используемого в социально-экономическом анализе, можно исчислить только одно истинное значение средней на базе, научного способа расчета. Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется один из видов средних величин: арифметическом, гармоническая, геометрическая, квадратическал, кубическая и т.д. Перечисленные средние относятся к классу степенных средних и объединяются общей формулой (при различных значениях т):
где х — среднее значение исследуемого явления; т — показатель степени средней; хi — текущее значение (вариант) осредняемого признака; n — число признаков. Далее пределы суммирования не указываются. В зависимости от значения показателя степени т различают следующие виды степенных средних: при т = -1 — средняя гармоническая xгр; при т = 0 — средняя геометрическая x г; при т = 1 — средняя арифметическая хар.; при т = 2 — средняя квадратическая хкв.; при т = 3 — средняя кубическая хкуб.. При использовании одних и тех же исходных данных, чем больше т в формуле (1.5.1), тем больше значение средней величины: xгр. ≤ xг. ≤ хар. ≤ хкв. ≤ хкуб. Это свойство степенных средних возрастать с повышением показателя степени определяющей функции называется в статистике правилом мажорантности средних. Характер имеющихся данных определяет существование только одного истинного среднего значения показателя. Вид средней выбирается в каждом отдельном случае путем конкретного анализа изучаемой совокупности, он определяется материальным содержанием изучаемого явления, а также принципами суммирования и взвешивания. Наиболее распространенным видом средних является средняя арифметическая. Она определяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Для общественных явлений характерна аддитивность (суммированность) объемов варьирующего признака, этим определяется область применения средней арифметической и объясняется ее распространенность как обобщающего показателя. Так, например: общий фонд заработной платы – это сумма заработных плат всех работников, валовой сбор урожая – сумма произведенной продукции со всей посевной площади. Чтобы исчислить среднюю арифметическую, нужно сумму всех значений признаков разделить на их число. Средняя арифметическая применяется в форме простой средней и взвешенной средней. Исходной, определяющей формой служит простая средняя. Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений (она применяется в тех случаях, когда имеются несгруппированные индивидуальные значения признака):
Хар. = х1 + х2 + … + хn / n = ∑х / n (1.5.2.) где х1, х2,…,хn – индивидуальные значения варьирующего признака (варианты); n — число единиц совокупности. Средняя из вариантов, которые повторяются различное число раз, или, как говорят, имеют различный вес, называется взвешенной. В качестве весов выступают численности единиц в разных группах совокупности (в группу объединяют одинаковые варианты).
Средняя арифметическая взвешенная – средняя сгруппированных величин х1, х2,…,хn – вычисляется по формуле.
Х = х1f1 + х2 f2 + … + хn fn / f1 + f2 + … +fn= ∑хf / ∑f (1.5.3) где f1, f2, …, fn – веса (частоты повторений одинаковых признаков); ∑хf – сумма произведений величины признаков на их частоты; ∑f - общая численность единиц совокупности. В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы). Тогда формула средней арифметической взвешенной будет иметь вид: Х = ∑хd / ∑d (1.5.4.) где d = f/ ∑f – частость, т.е. доля каждой частоты в общей сумме всех частот. Если частоты подсчитывают в долях (коэффициентах), то ∑d = 1, и формула средней арифметической взвешенной имеет вид: Х = ∑хd (1.5.5.) Часто приходится исчислять среднюю по групповым средним или по средним отдельных частей совокупности (частным средним), т.е. среднюю из средних. Так, например, средняя продолжительность жизни граждан страны представляет собой среднее из средних продолжительностей жизни по отдельным регионам данной страны. Средние из средних рассчитываются так же, как и средние из первоначальных значений признака. При этом средние, которые служат для исчисления на их основе общей средней, принимаются в качестве вариантов. Вычисление средней арифметической взвешенной из групповых средних х, осуществляется по формуле: Х = ∑хf / ∑f (1.5.6.) где f — число единиц в каждой группе. Если значения осредняемого признака заданы а виде интервалов ("от - до"), т.е. интервальных рядов распределения, то при расчете средней арифметической величины в качестве значений признаков в группах принимают середины этих интервалов, в результате чего образуется дискретный ряд. Вычисление средней арифметической часто сопряжено с большими затратами времени и труда. Однако в ряде случаев процедуру расчета средней можно упростить и облегчить, если воспользоваться ее свойствами. Приведем (без доказательства) некоторые основные свойства средней арифметической. Свойство 1. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю. ∑ (х – xaр.) = 0 Свойство 2. Если все индивидуальные значения признака (т.е. все варианты) уменьшить или увеличить в i раз, то среднее значение нового признака соответственно уменьшится или увеличится в i paз.
Свойство 3. Если все варианты осредняемого признака уменьшить или увеличить на число А, то средняя арифметическая соответственно уменьшится или увеличится на это же число А.
Свойство 4. Если веса всех осредняемых вариантов уменьшить или увеличить в к раз, то средняя арифметическая не изменится.
Для упрощения расчетов средней идут по пути уменьшения значений вариантов и частот. Наибольшее упрощение достигается, когда в качестве А выбирается значение одного из центральных вариантов, обладающего наибольшей частотой, в качестве i — величина интервала (применимо только для рядов с одинаковыми интервалами). Величина А называется началом отсчета, поэтому такой метод вычисления средней называется "способом отсчета от условного нуля" или "способом моментов";. Допустим, что все варианты х сначала уменьшены на одно и то же число А, а затем уменьшены в i раз. Получим новый вариационный ряд распределения новых вариантов х. Тогда новые варианты будут выражаться
а их новая средняя арифметическая m1 – момент первого порядка — формулой
и будет равна средней из первоначальных вариантов, уменьшенной сначала на А, затем в i раз. Для получений действительной средней надо момент первого порядка mi умножить на i и прибавить А:
Это и будет формула средней по способу моментов. Применяется этот способ в рядах с равными интервалами. Применение способа моментов настолько облегчает расчеты, что позволяет их выполнять без использования вычислительной техники даже при больших и многозначных числах, характеризующих индивидуальные значения осредняемых показателей. При расчете средних показателей помимо средней арифметической могут использоваться и другие виды средних. Однако любая средняя величина должна вычисляться так, чтобы при замене ею каждого варианта осредняемого признака не изменялся итоговый, обобщающий, или, как его принято называть определяющий показатель, который связан с осредняемым показателем (например, при замене фактических скоростей на отдельных отрезках пути их средней скоростью не должно измениться общее расстояние, пройденное транспортным средством за одно и то же время; при замене фактической заработной платы отдельных работников предприятия средней заработной платой, не должен измениться фонд заработной платы). Следовательно, в каждом конкретном случае в зависимости от характера имеющихся данных, существует только одно истинное среднее значение показателя, адекватное свойствам и сущности изучаемого социально-экономического явления. Вид средней определяется характером взаимосвязи определяющего показателя с осредняемым. Средняя арифметическая, как было показано выше, применяется в тех случаях, когда известны варианты варьирующего признака х и их частоты f. Когда статистическая информация не содержит частот f по отдельным вариантам х совокупности, а представлена как их произведение xf, применяется формула средней гармонической взвешенной. Чтобы исчислить среднюю, обозначим xf=M, откуда f=M/x. Теперь преобразуем формулу средней арифметической таким образом, чтобы по имеющимся данным х и М можно было исчислить среднюю. В формулу средней арифметической взвешенной (3.3.) вместо xf подставим М, вместо f — отношение М/х и получим формулу средней гармонической взвешенной:
где М = х× f. Из вышеприведенной формулы видно, что средняя гармоническая — средняя взвешенная из варьирующих обратных значений признака. Она является преобразованной формой арифметической средней и тождественна ей. Вместо гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужно определить веса отдельных значений признака, скрытые в весах средней гармонической. Таким образом, средняя гармоническая применяется тогда, когда неизвестны действительные веса f, а известно M=xf.
Исчисление средней гармонической взвешенной освобождает от необходимости предварительного расчета весов, поскольку эта операция заложена в формулу. В тех случаях, когда вес каждого варианта равен единице (т.е. индивидуальные значения обратного признака встречаются по одному разу), применяется средняя гармоническая простая, исчисляемая по формуле:
Если по двум частям совокупности (численности n1 и n2 ) даны средние гармонические, то общую среднюю гармоническую по всей совокупности можно представить как взвешенную гармоническую среднюю из групповых средних:
Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста. Средняя геометрическая исчисляется извлечением корня степени и из произведений отдельных значений — вариантов признака х: простая средняя геометрическая:
где n — число вариантов; П — знак произведения. взвешенная:
Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения. В ряде случаев в экономической практике возникает потребность расчета среднего размера признака, выраженного в квадратных или кубических единицах измерения, Тогда применяется средняя квадратическая (например, для вычисления квадратных участков, средних диаметров труб, стволов и т.п.) и средняя кубическая (например, при определении средней длины стороны и кубов). Средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:
|

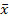 =
=  (1.5.1)
(1.5.1) =
= 

 A
A =
= 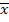
 =
= 
 =
= 
 =
=  (1.5.7.)
(1.5.7.) =
=  (1.5.8.)
(1.5.8.) =
=  . (1.5.9.)
. (1.5.9.) (1.5.10.)
(1.5.10.) =
=  =
=  (1.5.11.)
(1.5.11.) =
=  (1.5.12.)
(1.5.12.) =
=  =
=  . (1.5.13.)
. (1.5.13.)


