Средняя квадратическая взвешенная
где f - веса. Формулы для расчета средней кубической аналогичны: простая
Взвешенная
Средние квадратическая и кубическая имеют ограниченное применение в практике статистики. Широко пользуется статистика средней квадратической, но не из самих вариантов х, и из их отклонений от средней (х - 1с) при расчете показателей вариации. Средняя может быть вычислена не для всех, а для какой-либо части единиц совокупности. Примером такой средней может быть средняя прогрессивная как одна из частных средних, вычисляемая не для всех, а только для "лучших" (например, для показателей выше или ниже средних индивидуальных). Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана. Мода (Мо) – значение случайной величины, встречающееся с наибольшей вероятностью, в дискретном вариационном ряду это вариант, имеющий наибольшую частоту. В интервальных рядах распределения мода вычисляется по формуле:
где Хмо — нижняя граница модального интервала; iмо — модальный интервал; fмо, fмо+1, fмо-1 — частоты в модальном, предыдущем и следующем за модальным интервалах (соответственно). Модальный интервал определяется по наибольшей частоте. Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и т.п. Медиана (Me) — это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части — со значениями признака меньше медианы и со значениями признака больше медианы. Чтобы найти медиану необходимо отыскать значение признака, которое находится в середине упорядоченного ряда. В ранжированных рядах несгруппированных данных нахождение медианы сводится к отысканию порядкового номера медианы. В случае четного объема рада медиана равна средней из двух вариантов, находящихся в середине рада.
В интервальных рядах распределения медианное значение (поскольку оно делит всю совокупность на две равные по численности части) оказывается в каком-то из интервалов признака х. Этот интервал характерен тем, что его кумулятивная частота (накопленная сумма частот) равна или превышает полусумму всех частот ряда. Значение медианы вычисляется линейной интерполяцией по формуле: Me = Xме + iме × (∑f/2 – Sме-1) / fме (1.5.18.) где Xме – нижняя граница медианного интервала; iме – медианный интервал; ∑f/2 – половина от общего числа наблюдений; Sме-1 – сумма наблюдений, накопленная до начала медианного интервала; fме – число наблюдений в медианном интервале. Формула (5.3.14) получена исходя из допущения о равномерности нарастания накоплений частоты внутри интервала и пригодна для любого интервального ряда. Медиана находит практическое применение в маркетинговой деятельности вследствие особого свойства — сумма абсолютных отклонений чисел ряда от медианы есть величина наименьшая: ∑(x – Me) min. Мода и медиана в отличие от степенных средних являются конкретными характеристиками, их значение имеет какой-либо конкретный вариант в вариационном ряду. Мода и медиана, как правило, отличаются от значения средней, совпадая с ней только в случае симметричного распределения частот вариационного рада. Поэтому соотношение моды, медианы и средней арифметической позволяет оценить ассиметрню ряда распределения. Мода и медиана, как правило, являются дополнительными характеристиками совокупности и используются в математической статистике для анализа формы радов распределения. Аналогично медиане вычисляются значения признака, делящие совокупность на четыре равные (по числу единиц) части – квартели, на пять равных частей – квинтели, на десять частей – децели, на сто частей – перцентели. Использование в анализе вариационных рядов распределения, рассмотренных выше характеристик, позволяет более глубоко и детально охарактеризовать изучаемую совокупность.
|

 =
=  ; (1.5.14.)
; (1.5.14.) =
= 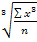 ; (1.5.15.)
; (1.5.15.) . (1.5.16.)
. (1.5.16.) =
= 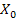 +
+ 

 ; (1.5.17.)
; (1.5.17.) −
−  .
.


