Оценка статистической совокупности
Контрольная работа
По предмету: Статистика
На тему: Статистический анализ
Выполнил: Проверила:
студент гр. УП-211 ассистент кафедры
Брылунова Н.Д. Кушнарева Л.В.
Екатеринбург
Начальный этап построения ряда распределения заключается в проверке качества исследуемой статистической совокупности. Неоднородность совокупности – следствие значительной вариации признака и сильного различия условий, влияющих на формирование характеристик единиц совокупности. Резко выделяющиеся (≪аномальные≫) значения признака не позволяют на достаточно высоком уровне оценить и проанализировать статистические данные.
Для оценки однородности (качества) совокупности составляется таблица 1.1.
Таблица 1.1 – Определение средних степенных величин статистической совокупности
| № Предприятия
| Стоимость основных средств
| Расчетная графа
| | | xi
| 
| |
| 5,9
| 0,334
| |
| 5,9
| 0,334
| |
| 7,8
| 1,748
| |
| 6,7
| 0,049
| |
| 7,8
| 1,748
| |
| 6,2
| 0,077
| |
| 6,1
| 0,143
| |
| 7,4
| 0,850
| |
| 4,3
| 4,744
| |
| 6,0
| 0,228
| |
| 6,2
| 0,077
| |
| 6,5
| 0,000
| |
| 7,3
| 0,676
| |
| 6,4
| 0,006
| |
| 6,6
| 0,015
| |
| 7,2
| 0,521
| |
| 7,0
| 0,272
| |
| 6,2
| 0,077
| |
| 6,6
| 0,015
| |
| 7,2
| 0,521
| |
| 7,3
| 0,676
| |
| 6,7
| 0,049
| |
| 7,6
| 1,259
| |
| 7,6
| 1,259
| |
| 5,6
| 0,771
| |
| 7,5
| 1,044
| |
| 5,8
| 0,460
| |
| 4,7
| 3,161
| |
| 7,3
| 0,676
| |
| 6,2
| 0,077
| |
| 7,6
| 1,259
| |
| 6,3
| 0,032
| |
| 5,9
| 0,334
| |
| 5,8
| 0,460
| |
| 6,0
| 0,228
| |
| 7,7
| 1,493
| |
| 6,8
| 0,104
| |
| 5,2
| 1,633
| |
| 5,9
| 0,334
| |
| 6,9
| 0,178
| |
| 7,2
| 0,521
| |
| 5,7
| 0,605
| |
| 6,1
| 0,143
| |
| 6,7
| 0,049
| |
| 6,3
| 0,032
| |
| 6,7
| 0,049
| |
| 6,2
| 0,077
| |
| 6,3
| 0,032
| |
| 5,1
| 1,899
| |
| 5,9
| 0,334
| | ∑
| 323,9
| 31,7
|
Проверка совокупности предполагает использование следующих двух методов:
1) Расчет коэффициента вариации по формуле:

где 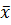 – средняя арифметическая простая величина, характеризующая совокупность, рассчитывается по формуле: – средняя арифметическая простая величина, характеризующая совокупность, рассчитывается по формуле:

 - среднее квадратическое отклонение индивидуальных значений признака от их средней величины, рассчитывается по формуле: - среднее квадратическое отклонение индивидуальных значений признака от их средней величины, рассчитывается по формуле:

Значение коэффициента вариации меньшее 33,3 % свидетельствует о том, что совокупность однородная и построенный по ней ряд распределения будет значимым. Значение большее 33,3 % говорит о том, что совокупность неоднородна и из нее необходимо убрать резко выделяющиеся наблюдения.
Для расчета средней арифметической и показателей вариации заполняется таблица 2.1. В рассматриваемом примере искомые средние степенные величины примут значения:


Коэффициент вариации составит:

Так как расчетное значение коэффициента вариации меньше 33,3 % (11,9% < 33,3 %), то совокупность признается однородной.
2) Использование правила ≪трех сигма≫, которое заключается в соблюдении следующего интервала:
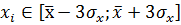
Таким образом, любое индивидуальное значение признака должно попадать в интервал. Если некоторые значения в этот интервал не входят, то они исключаются из изучаемой совокупности и все средние величины и показатели вариации пересчитываются заново.
В рассматриваемом примере все значения стоимости основных средств входят в искомый интервал:

Так как минимальное значение стоимости основных средств по совокупности больше нижней границы интервала ≪трех сигма≫ (4,3 > 4,091), максимальное значение меньше верхней границы (7,8< 8,865), можно сделать вывод что ≪аномальных≫ наблюдений нет и совокупность однородна.
1.2. Построение ряда распределения и расчёт его основных характеристик
Ряд распределения состоит из двух элементов – варианты и частоты (и/или частности). Варианта – значение изучаемого признака, находящегося в определенных границах. Величина варианты (интервала) зависит от размаха вариации и количества групп, на которые разбивается совокупность. Значение варианты рассчитывается по формуле (1.1). При этом количество интервалов (п) определяется по формуле Стерджесса:

При величине совокупности (N) равной пятидесяти, количество интервалов составит:

Тогда варианты составят:

и ряд распределения примет вид:
Таблица 1.2 – Ряд распределения предприятий по величине торговой площади
| группы (варианты) показателей по вел-не стоимости основных средств, млн.руб
| кол-во показателей в группе
| расчетные графы
| | серед.интервала
|
| накоплен. частота
| | xi
| fi
| x'i
| x'i fi
| Si
| | 4,3-4,8
|
| 4,55
| 9,1
|
| | 4,8-5,3
|
| 5,05
| 10,1
|
| | 5,3-5,8
|
| 5,55
| 22,2
|
| | 5,8-6,3
|
| 6,05
| 96,8
|
| | 6,3-6,8
|
| 6,55
| 58,95
|
| | 6,8-7,3
|
| 7,05
| 63,45
|
| | 7,3-7,8
|
| 7,55
| 60,4
|
| | Сумма
|
|
|
|
| Графически ряд распределения изображен на рисунке 1.1.

а) гистограмма

б) полигон
Рисунок 1.1. – Ряд распределения предприятий по величине стоимости основных средств.

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|
Психолого-педагогическая характеристика студенческой группы
Характеристика группы составляется по 407 группе очного отделения зооинженерного факультета, бакалавриата по направлению «Биология» РГАУ-МСХА имени К...
Общая и профессиональная культура педагога: сущность, специфика, взаимосвязь Педагогическая культура- часть общечеловеческих культуры, в которой запечатлил духовные и материальные ценности образования и воспитания, осуществляя образовательно-воспитательный процесс...
Устройство рабочих органов мясорубки Независимо от марки мясорубки и её технических характеристик, все они имеют принципиально одинаковые устройства...
|
Этапы творческого процесса в изобразительной деятельности По мнению многих авторов, возникновение творческого начала в детской художественной практике носит такой же поэтапный характер, как и процесс творчества у мастеров искусства...
Тема 5. Анализ количественного и качественного состава персонала Персонал является одним из важнейших факторов в организации. Его состояние и эффективное использование прямо влияет на конечные результаты хозяйственной деятельности организации.
Билет №7 (1 вопрос) Язык как средство общения и форма существования национальной культуры. Русский литературный язык как нормированная и обработанная форма общенародного языка Важнейшая функция языка - коммуникативная функция, т.е. функция общения Язык представлен в двух своих разновидностях...
|
|



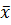 – средняя арифметическая простая величина, характеризующая совокупность, рассчитывается по формуле:
– средняя арифметическая простая величина, характеризующая совокупность, рассчитывается по формуле:
 - среднее квадратическое отклонение индивидуальных значений признака от их средней величины, рассчитывается по формуле:
- среднее квадратическое отклонение индивидуальных значений признака от их средней величины, рассчитывается по формуле: