Ошибки выборки средних величин
Рассмотрим определение ошибки выборки для абсолютных величин на примере уточнения значения средней арифметической простой величины. Средняя ошибка выборки (μ) обеспечивает надежность средней величины с точностью 0,683 и рассчитывается по формуле:
где n – величина выборочной совокупности, N – величина генеральной совокупности. Зная, что n=50 является двадцатипроцентной выборочной совокупностью, можно рассчитать величину генеральной совокупности.
Тогда средняя ошибка выборки составит:
Предельная ошибка выборки (
где t – коэффициент кратности средней ошибки выборки, определяемый по таблице в приложении А. При вероятности возникновения ошибки равной 0,95 коэффициент доверия составляет t(0,954) =2. Значит, предельная ошибка выборки примет значение:
Доверительный интервал средней арифметической находится в границах:
Таким образом, можно гарантировать с вероятностью 0,954, что средняя величина стоимости основных средств в генеральной совокупности не будет меньше 6,4 млн.руб. и не превысит 1.3.2. Ошибки выборки долей статистической совокупности Ошибку выборки для относительных характеристик рассмотрим на примере удельной доли предприятий, акционерный капитал которых превышает его среднюю величину (w = 0,5 = 50%). Средняя ошибка для доли совокупности рассчитывается по формуле:
Предельная ошибка выборки также рассчитывается с учетом вероятности ее возникновения (при P = 0,975, t=2,24 из приложения А):
Доверительный интервал доли генеральной совокупности определяется в границах:
Значит количество предприятий, товарная площадь которых больше среднего, в генеральной совокупности составит не меньше 35,8 % и не превысит 64,1 %.
|




 ) уточняет среднюю ошибку на коэффициент, определенный вероятностью ее возникновения:
) уточняет среднюю ошибку на коэффициент, определенный вероятностью ее возникновения:

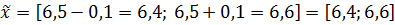
 6,6 млн.руб.
6,6 млн.руб.








