Показатели размера и интенсивности вариации признаков единиц совокупности
Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным относятся размах вариации (R), среднее линейное отклонение ( Относительными показателями вариации являются коэффициент осцилляции, вариации, относительное линейное отклонение, относительный показатель квартильной вариации и др. Они вычисляются как отношение абсолютных показателей вариации к средней арифметической или медиане. Самым простым абсолютным показателем является размах вариации. Его исчисляют как разность между наибольшим и наименьшим значениями варьирующего признака.
Величина R всецело зависит от крайних значений признака, и он не учитывает всех изменений варьирующего признака в пределах совокупности Более точно характеризуют вариацию признака показатели, основанные на учете колеблемости всех значений признака, - среднее линейное отклонение (d) и среднее квадратическое отклонение (δ). Распределение отклонений можно уловить, исчислив о тклонения всех вариант от средней. Отклонение от средней - это разность между вариантой (х) и средней арифметической ( Чтобы исчислить среднее арифметическое из отклонений нужно применить формулу средней арифметической: а) простую
|
), дисперсия (δ2), среднее квадратическое отклонение (δ), квартильное отклонение Q.
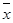) в данной совокупности.
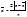; б) взвешенную 
.
= 
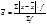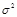