Типовые задачи для подготовки к зачетной работе (итоговой по курсу).
1. Найдите соотношения цен трех товаров, если стоимости наборов 2. Найдите наибольшее значение функции ∆(x) на отрезке [-4, 4]:
3. Решите систему уравнений:
4. Найдите собственные значения и собственные векторы линейного оператора, заданного матрицей А. Найти косинус угла между линейно независимыми собственными векторами матрицы.
5. Найдите значение параметра a, при котором бесконечно малые функции (1-cosx) и a sin2x будут эквивалентными при 𝑥 →0.
6. Дана функция а) Найдите все асимптоты графика функции. б)Найдите точки экстремума и перегиба, промежутки монотонности и выпуклости вверх/вниз. в) Нарисуйте эскиз графика функции: г) Напишите уравнение касательной к графику функции д) Найдите площадь фигуры, ограниченной графиком функции 7. Найти матрицу 8. Доказать, что данные векторы линейно независимы: 9. Найти матрицу линейного отображения 10. Вычислите пределы: а) 11. Найдите интегралы: а) 12. Дана функция: z =x2-2xy +4y3. а) Вычислите dz |M при dx=∆x=-0.1, dy=∆y=0.1, M=(1,1). Найдите с помощью первого дифференциала приближенно z(0.9; 1.1). б) Найдите все стационарные точкифункции z. Проверьте выполнение достаточных условий в одной стационарной точке. 13. Используя метод Лагранжа,найти точки локального экстремума функции z=5-2x +3 y при условии x 2 +4y 2 =100. Проверьте выполнение достаточных условий в одной стационарной точке. Постройте график условия.
14. На основе опытных данных установлены зависимости спроса q (количество покупаемого товара) и предложения s (количество предлагаемого на продажу товара) от цены товара p:
Определите эластичность спроса по равновесной цене, изменение спроса при увеличении цены на 5% от равновесной. 15. Найдите наибольшее и наименьшее значения функции z=1- x2-y2 в круге (x-1)2 +(y-1)2≤1. Постройте линии уровня функции z, проходящиечерез точки, в которых z принимает наибольшее и наименьшее значения в круге.
|

 , этих товаров относятся как 9:7:5.
, этих товаров относятся как 9:7:5.


 .
. из уравнения
из уравнения  .
. .
. , если А – вращение по часовой стрелке на 180˚ относительно начала координат.
, если А – вращение по часовой стрелке на 180˚ относительно начала координат.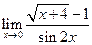 ; б)
; б)  .
. ; б)
; б)  .
.



