Контрольная работа №2
Вариант№1 1. Найдите производные для указанных функций.
a) в) 2. Найти скорость изменения функции у = (х2 + 2)* (х – 1) при у = 6. 3. Измерения прямоугольного параллелепипеда 15, 50 и 36 м. Найти ребро равновеликого ему куба. 4. Основанием пирамиды служит равнобедренный треугольник, у которого, основание равно 12 см, а боковая сторона 10 см. Боковые грани образуют с основанием равные двугранные углы, содержащие по 45°. Определить высоту этой пирамиды и ее объем. 5. Высота цилиндра на 10см больше радиуса основания, а полная поверхность равна 144 6. Решите уравнения: a) b)
7. Вычислите 8. Упростите: 9. Вычислите: 10. Постройте график функции:
Вариант №2 1. Найдите производные функций a) в)
2. Основание параллелограмма изменяется о закону а = (2 + 3t) см, а высота h по закону h =(3t - 1) см. Определить скорость изменения его площади в момент t = 2с. 3. В прямом параллелепипеде стороны основания равны 6 и 8 см, угол между ними 30°. Площадь полной поверхности равна 188 см2. Определить объем параллелепипеда. 4. Основанием пирамиды служит равнобедренный треугольник, у которого основание равно 6 см и высота 9 см; боковые ребра равны между собой, и каждое содержит, 13 см. Определить объем этой пирамиды. 5. Цилиндрическая дымовая труба с диаметром 65 см имеет высоту в 18 см. Сколько квадратных метров жести нужно для ее изготовления, если на заклепку уходит 10% площади трубы. 6. Решите уравнения: a) b)
7. Вычислите: 8. Вычислите: 9. Упростите: 10. Постройте график функции: у=
Вариант №3 1. Найдите производную функции a. a) b. в)
2. Маховик, задерживаемый тормозом, за t секунд поворачивается на угол 3. В прямой треугольной призме стороны основания равны 6см, 25 см и 29 см, площадь полной ее поверхности равна 1560см. Вычислить объем призмы. 4. Основанием пирамиды служит треугольник со сторонами 39 см, 17 см и 28 см; боковые ребра равны каждое 22,9 см. Определить объем этой пирамиды. 5. Жидкость, налитая в конический сосуд, имеющий 0,18 м высоты и 0,24 м в диаметре основания, переливается в цилиндрический сосуд, диаметр основания которого 0,10 м. Как высоко будет стоять уровень жидкости в сосуде? 6. Решите уравнения: a) b) 7. Вычислите: 8. Вычислите: 9. Упростите: 10. Постройте график функции: у=
Вариант №4 1. Найдите производную функции a) i. в) 2. Найти силу тока I в момент времени t = 5, если Q = 6 t3- 4 t2+ 1 (I – в амперах, t – в секундах). 3. В прямом параллелепипеде стороны основания 18 см и 34 см; меньшая диагональ основания 20 см. Меньшая диагональ параллелепипеда образует с плоскостью основания угол 60°. Вычислить объем этого параллелепипеда. 4. Гранитная подставка имеет вид усеченной пирамиды высотой в 3,6 м с 5. Ребра прямоугольного параллелепипеда 4 см, 6 см, 12 см. Найти объем описанного шара и площадь сферы. 6. Решите уравнения: a) b)
7. Найдите 8. Докажите тождество: 9. Вычислите: 10. Постройте график функции: у=
Вариант №5 1. Найдите производную функции a) в) 2. Сила тока изменяется в зависимости от времен t по закону I = 0,4 t2 + 4 t (I – в амперах, t – в секундах). Найти скорость изменения силы тока в конце 8-й секунды. 3. В прямой треугольной призме стороны основания равны 25 см, 29 см и 4. Основанием пирамиды служит равнобедренный треугольник, у которого равные стороны содержат по 39 см, а третья сторона 30 см. Двугранные углы при основании равны между собой, и каждый содержит 45°. Определить объем этой пирамиды. 5. Куча щебня имеет коническую форму, радиус основания которой 2 м и 6. Решите уравнения: a) b)
7. Найдите 8. Докажите тождество: 9. Вычислите: ctg 10. Постройте график функции: у=
Вариант №6 1. Найдите производную функции a) в) 2. Изменение силы тока I в зависимости от времени t задано уравнением I = 2 t2 - 5 t (I – в амперах, t – в секундах). Найти скорость изменения силы тока в конце 10-й секунды. 3. В прямом параллелепипеде стороны основания равны 6 см и 8 см, угол 4. Основание пирамиды – прямоугольный треугольник, один из катетов 5. Полуцилиндрический свод подвала имеет 6 м длины и 5,8 м в диаметре. Определить полную поверхность подвала. 6. Решите уравнения: a) b) 7. Найдите 8. Докажите тождество: 9. Вычислите: 10. Постройте график функции: у=
Вариант №7 1. Найдите производную функции a) в) 2. Температура тела T изменяется в зависимости от времен t по закону T = 0,5 t2 - 2 t. С какой скоростью нагревается это тело в момент времени t =5с. 3. Основание прямого параллелепипеда - параллелограмм, стороны которого 9см и 10см, а одна из диагоналей 17см. Площадь полной поверхности параллелепипеда равна 334см2. Определить его объем. 4. В цилиндре радиус основания равен 2 см, а высота равна 7 см. Найти 5. Высота и образующая конуса относятся как 4:5, а объем конуса равен 6. Решите уравнения: a) b) 7. Найдите 8. Докажите тождество: 9. Вычислите: 10. Постройте график функции: у=
Вариант №8 1. Найдите производную функции a. a) b. в) 2. Тело движется прямолинейно по закону S= 1/6 t3 + 3 t2 – 5 (S - в метрах, t – в секундах). Найти скорость движения в момент времени, когда ускорение равно 0. 3. В прямоугольном параллелепипеде боковое ребро равно 5см, площадь диагонального сечения 205 см2 и площадь основания 360 см2. Определить стороны основания параллелепипеда. 4. В правильной четырехугольной усеченной пирамиде апофема равна 12 см, боковое ребро равно 13 см и площадь боковой поверхности равна 720 см2.Определить стороны оснований. 5. Крыша силосной башни имеет форму конуса. Высота крыши 2 м. Диаметр башни 6 м. Сколько листов кровельного железа потребовалось для покрытия крыши, если лист имеет размеры 0,7x1,4 (м2) и на швы пошло 10% требующегося железа? 6. Решите уравнения: a) b)
7. Вычислите: 8. Вычислите: 9. Упростить: 10. Постройте график функции: у=
Вариант №9 1. Найдите производную функции a) в) 2. Сставьте уравнение касательной, проведенной к графику функции у = х3+2х2- 4х- 3 в точке с абсциссой х = -2. 3. В прямой треугольной призме стороны основания равны 6см, 25 см и 29 см, площадь полной ее поверхности равна 1560см. Вычислить объем призмы. 4. Основанием пирамиды служит треугольник со сторонами 39 см, 17 см и 28 см; боковые ребра равны каждое 22,9 см. Определить объем этой пирамиды. 5. Жидкость, налитая в конический сосуд, имеющий 0,18 м высоты и 0,24 м в диаметре основания, переливается в цилиндрический сосуд, диаметр основания которого 0,10 м. Как высоко будет стоять уровень жидкости в сосуде? 6. Решите уравнения: a) b) 7. Найдите 8. Вычислите: 9. Упростить: 10. Постройте график функции: у=
Вариант№10 1. Найдите производную функции a) в)
2. Составьте уравнение касательной, проведенной к графику функции у = 3 х2-2х+1 в точке с абсциссой х = 0,5. 3. В прямой треугольной призме стороны основания равны 6см, 25 см и 29 см, площадь полной ее поверхности равна 1560см. Вычислить объем призмы. 4. Основанием пирамиды служит треугольник со сторонами 39 см, 17 см и 28 см; боковые ребра равны каждое 22,9 см. Определить объем этой пирамиды. 5. Жидкость, налитая в конический сосуд, имеющий 0,18 м высоты и 0,24 м в диаметре основания, переливается в цилиндрический сосуд, диаметр основания которого 0,10 м. Как высоко будет стоять уровень жидкости в сосуде? 6. Решите уравнения: a) b) 7. Найдите 8. Докажите тождество: 9. Вычислите: 10. Постройте график функции: у=
|

 ; б)
; б)  ;
; ; г)
; г)  .
. см2. Определить объем цилиндра.
см2. Определить объем цилиндра.


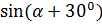 .если
.если 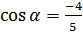
 .
.


 ; б)
; б)  ;
; ; г)
; г) 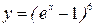 .
.

 ,
,  если
если  ,
, 



 ; б)
; б)  ;
; ; г)
; г)  .
. = 5 t – 0,4 t2 (рад). Определить скорость
= 5 t – 0,4 t2 (рад). Определить скорость  маховика в момент времени t = 2с и найти момент, когда вращение прекратиться.
маховика в момент времени t = 2с и найти момент, когда вращение прекратиться.

 ,
,  и
и 

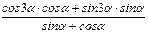

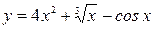 ; б)
; б)  ;
; ; г)
; г)  .
.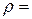 2,5 т/м3.
2,5 т/м3.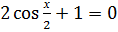
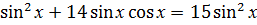
 , если
, если 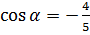 и
и 


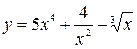 ; б)
; б)  ;
; ; г)
; г)  .
.
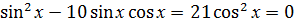
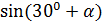 , если
, если 


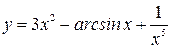 ; б)
; б)  ;
; ; г)
; г)  .
.

 , если
, если  и
и 
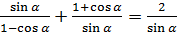

 ; б)
; б)  ;
; ; г)
; г)  .
. см2. Найти площадь полной поверхности конуса
см2. Найти площадь полной поверхности конуса

 , если
, если  и
и 


 ; б)
; б) 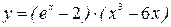 ;
; ; г)
; г)  .
.
 ; б)
; б)  ;
;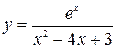 ; г)
; г)  .
.

 ; б)
; б)  ;
;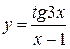 ; г)
; г)  .
.



