Регрессионный анализ.
Регрессионный анализ – статистический метод установления формы и изучения связей между метрически зависимой переменной и одной или несколькими независимыми переменными. Регрессионный анализ используется, если необходимо: уточнить действительно ли переменные взаимосвязаны, определить форму связи, предсказать значения зависимой переменной, определить в какой степени вариацию зависимой переменной можно объяснить независимыми переменными (теснота связи). Парная регрессия – метод установления математической зависимости между 2 метрическими переменными. Этапы: 1) Построение поля корреляции (диаграммы рассеяния) – графического представления точек с координатами, определяемыми значениями 2-х переменных для всех наблюдений. Поле корреляции показывает, можно ли зависимость Y по X выразить прямой линией и, следовательно, подходит ли к этим данным парная регрессионная модель. 2) Формулирование модели. Модель парной регрессии 3) Вычисление параметров. В большинстве случаев 4) Вычисление нормированного коэффициента регрессии (бета-коэфициента) – показывающего изменение Y в зависимости от изменения X (угол наклона прямой уравнения регрессии), при условии, что все данные нормированы. 5) Проверка значимости. Исследование гипотез Но (β1=0) и Н1 (β1≠0). 6) Определение тесноты и значимости связи. Коэффициент детерминации (r2) - статистический показатель, характеризующий тесноту связи между метрическими переменными. В пределах от 0 до 1 – указывает на долю полной вариации, которая обусловлена вариацией Х. 7) Проверка точности предсказаний. Чтобы оценить точность предсказанных значений Y полезно вычислить стандартную ошибку оценки уравнения регрессии SEE, которая представляет собой стандартное отклонение фактических значений Y от теоретических значений. При наличии k независимых переменных: SEE= 8) Анализ остатков. Остаток – разность между наблюдаемым значением Y и его теоретическим значением, предсказанным уравнением регрессии. Анализ производится для подтверждения того, что модель регрессии подходит для анализа, с этой целью используется графический метод. 9) Перекрестная проверка модели.
|

 где
где  – точка пересечения прямой регрессии с 0У;
– точка пересечения прямой регрессии с 0У; 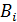 – тангенс угла наклона прямой;
– тангенс угла наклона прямой;  – остаточный член связанный с i-тым наблюдением характеризующий отклонение от функции регрессии; X–независимая переменная (предиктор);
– остаточный член связанный с i-тым наблюдением характеризующий отклонение от функции регрессии; X–независимая переменная (предиктор);  – зависимая.
– зависимая. = a+bx, где a и b – вычисляемые оценки Во и Вi. B- нормированный коэфициент регресии, показывающий ожидаемое изменение Y при изменении Х на единицу.
= a+bx, где a и b – вычисляемые оценки Во и Вi. B- нормированный коэфициент регресии, показывающий ожидаемое изменение Y при изменении Х на единицу.  ,
, 
 , Byx= ryx
, Byx= ryx , где SE – стандартная ошибка коэффициента регрессии (стандартное отклонение b).
, где SE – стандартная ошибка коэффициента регрессии (стандартное отклонение b). . SSy=SSрегрессии+SSошибки. SSy=
. SSy=SSрегрессии+SSошибки. SSy=  , SSрегрессии=
, SSрегрессии=  , SSошибки=
, SSошибки=  . Проверка значимости r^2. Гипотезы: Н0: r^2=0; Н1:r^2>0. Проверка проводится путем определения F-статистики.
. Проверка значимости r^2. Гипотезы: Н0: r^2=0; Н1:r^2>0. Проверка проводится путем определения F-статистики. 
 . Предполагается, что можно ожидать, что примерно 2/3 точек данных будут находится на расстоянии не более SEE выше или ниже регрессии. Ококло 95% значений данных должны находится на расстоянии не более чем 2х SEE от линии регрессии.
. Предполагается, что можно ожидать, что примерно 2/3 точек данных будут находится на расстоянии не более SEE выше или ниже регрессии. Ококло 95% значений данных должны находится на расстоянии не более чем 2х SEE от линии регрессии.


