Оценка регрессионной модели. Проверка адекватности модели регрессии.
Перекрестная проверка – проверка достоверности модели, с помощью которой изучают, применима ли регрессионная модель для анализа сопоставимых данных, не использовавшихся при построении исходной модели. Двойная проверка – специфическая форма проверки, в которой выборку делят на две равные части. Одна служит расчетной выборкой, а вторая – контрольной. Затем роли выборок меняются и проверку повторяют. Процедура перекрестной проверки: 1) расчет регрессионной модели на основе всего набора данных; 2) формирование расчетной и контрольной выборок; 3) Расчет регрессионной модели на основе данных из расчетной выборки и ее сравнение с моделью, рассчитанной по данным полной выборки, на предмет соответствия знаков и величин частных коэффициентов регрессии; 4) определяют значения зависимой переменной y для наблюдения в контрольной выборке; 5) рассчитывают линейный коэффициент детерминации r2 и сравнивают его с коэффициентом R2 для полной и расчетной выборки. Проверка адекватности модели регрессии. Процесс верификации модели – процесс, в ходе которого подвергается анализу качественно полученной модели, которая характеризуется выполнением определенных статистик и точностью, т.е. степенью близости к фактическим данным. Оценить адекватность модели позволяет анализ случайной компоненты ej. Модель считается адекватной исследуемому процессу, если 1) Математическое ожидание значений остаточного ряда близко или равно нулю 46. Дискриминантный анализ (ДА): цели, этапы выполнения ДА – анализ различий заранее определ групп объектов исслед. (тов., потреб., ТМ и т.д.). Д переменные – признаки, по кот изучаются различия между 2/более группами. Переменная, разд-щая сов-ть объектов исслед на группы, – группирующая перем. Цели ДА: 1) опр-ние Д ф-ций или лин комбинаций независ перем., кот наилучшим обр различают группы зависимой; 2) проверка сущ-ния между группами знач различий с т.зр независ.; 3) опр-ние предикторов, вносящих наиб вклад в межгрупп различия; 4) отнесение случаев к 1 из групп с учетом значений предикторов; 5) оценка точности классиф-ции данных на группы. Этапы ДА: 1 этап. Формул-ние проблемы: опр-ние целей, завис и независ переменных. Зависимая должна состоять из 2/более взаимоискл категорий, дб категориальной (если интерв./ относит., необх перевести в категориальную). 2 этап. Опр-ние коэфф-в Д ф-ции. Д ф-ция – лин комбинация независперем., выведенная посредством ДА, позвол наилучшим обр различить категории завис n. d=a+b1x1+b2x2, где d-группирующая перем., b1,2- коэфф-ты Д ф-ции, x1,2- независ перем. 2 метода выбора независ перем.: 1) прямой – одновр введение всех предикторов; 2) пошаговый – послед введение предикторов. Порядок опр-ния коэфф-в Д ф-ции: 1) опр-ся значения Д ф-ции (f) для каждого i-ого наблюд., кот опис-ся m переменными; 2) рассч-ся ср значение f для каждой группы; 3) опр-ся коэфф-ты Д ф-ции (bi), чтобы ср значения f1, f2 как можно больше отлич между собой. Константа Д – граница, разд-щая 2 множества. С=1/2(f1ср+f2ср). Объекты, распол над разд поверх-тью f(x)=c отнесены к 1 группе, а ниже – ко 2 группе. 3 этап. Опр-ние значимости Д ф-ции. Стат проверка Но о равенстве средних всех Д ф-ций во всех группах ген сов-ти базир-ся на коэфф лямбда λ Уилкса. Коэфф лямбда λ для каждого предиктора – отношение внутригрупп суммы квадратов к общей сумме квадратов. Если λ→1, то сред значения исслед групп не отличаются друг от друга. Если λ→0, это указывает на различия сред значений в группах, что позволяет отклонить Но. 4 этап. Интерпретация получ рез-тов. Преставление рез-тов нач-ся с обзора действит и пропущ значений (программа строит Д ф-цию, исп-я только действ знач.). Далее анал-ся λ и стат значимость. Значение стат-ки дб меньше 0,05 (это значит, что различия между средними знач Д переменных явл-ся стат знач.). Далее исследуем незав переменные на мультиколл., рассчитав коэфф корреляции (при наличии корреляции удаляем их). Далее анализируем коэфф-ты Д ф-ции. Канонич корреляция – амера связи между единств Д ф-цией и набором фикт перем., кот опр-т принадл-ть к дан группе. Собств значение ф-ции – отношение межгрупп суммы квадратов к внутригр сумме квадратов. Большие собств знач указывают на ф-ции более ↑ порядка (↑ качество модели). Для оценки вклада отд перем в значение Д ф-ции исп-ся стандарт коэф Д ф-ции. Далее строится структ матрица – объединение корееляции внутри групп между Д перем и стандартиз канонич Д ф-циями. Структ коэфф-ты корреляции – лин коэфф-ты корреляции между предикторами и Д ф-цией. Затем опр-ся нестанд коэфф-ты Д ф-ции, кот исп-ся для построения Д модели. Она должна максимально четко разделять исслед группы. 5 этап. Оценка достоверности ДА. Она оценив-ся по рез-там классиф-и, т.е. распределения объектов исслед по исслед группам. Выборка→ опр-ние дискр пок-лей→ распр-ние случаев по группам: верно/ ошибочно классифицир.→ расчет коэфф-та результ-ти. Коэфф-т результ-ти – % случаев, верно классиф-х с помощью ДА. Полезно сравнить % случаев, верно классиф-х с пом ДА, с % случаев, кот можно получить случ образом. % случаев класс-ции опр-ся делением 1 на кол-во групп. Счит-ся, что точность класс-ции, достигн с пом ДА, дб на 25% ↑, чем точность, кот можно достигнуть случ образом.
48. Кластерный анализ (КА): суть метода, этапы выполнения анализа, вращение факторов. КА – сов-ть методов, позвол классиф-ть многомерные наблюдения, каждое из кот опис-ся набором исходных переменных. КА – класс методов, исп-ся для класс-ции объектов или событий в относит однород группы – кластеры. Объекты в каждом кластере дб похожи друг на друга и отличаться от объектов в др кластерах. Элементы, вкл в 1 кластер, имеют разную ст схожести. Техника КА – в выявлении ур схожести всех исслед элементов и послед объединении элементов в порядке ↑ ур различия между ними. Число выявленных кластеров зависит от заданного ур схожести элем., вкл в 1 кластер. Цели КА: 1) сегментация рынка; 2) понимание потр поведения; 3) опр-ние возм-ти нов товаров; 4) выбор тестовых рынков; 5) ↓ размерности данных при создании кластеров. Этапы КА: 1 этап. Формул-ние проблемы. Осущ-ся выбор переменных. Для этого анализ-ся прошлое исслед., принимается во внимание раб гипотеза. Главная задача – набор перем должен описывать сходство между объектами с т.зр признаков, имеющих отношение к проблеме исслед. 2 этап. Опр-ние метода кластеризации. 2 метода: иерархич., неиерарх. Иерархический метод – метод класт-ции, хар-ся постр иерарх (древовид.) стр-ры. Подходы: 1) сверху вниз: все объекты→ в 1 кластер, затем раздел-ся, 2) снизу вверх: каждый объект – в своем кластере, затем они объедин. +: легкая интерпретация рез-тов, -: нестабильность. Неиерархический метод базируется на опр-нии центра кластера, после чего все объекты, попад в заранее опред пороговое расстояние от него, вкл-ся в этот кластер. На практике часто исп-ся сочетание 2 подходов. Иерархические методы: 1) агломеративные, 2) дивизионные. 1) Агломер. (каждый объект первоначально находится в отд кластере, далее групп-ся во все более крупные кластеры): методы связи, дисперсионные, центроидные. Методы связи объединяют объекты в кластер, исходя из вычисл расст-ния между ними (метод одиночной, полной, средней связи). Дисперсионные методы – кластер формир-ся так, чтобы минимиз внутрикласт дисперсию. Метод Варда – кластеры формир-ся т.о., чтобы минимиз квадраты евклидовых расстояний до кластерных средний. Центроидный метод – расстояние между 2 кластерами – расстояние между их центроидами – точками, координ кот явл-ся средними по всем наблюд в кластере. Объедин групп произв-ся в соотв с расстоянием между их центроидами, где это расст-ние минимально – первые группы. 2) Дивизионные – все объекты сначала входят в 1 кластер, далее кластер делится на более мелкие. Неиерархические методы: 1) последоват пороговый, 2) параллельный пороговый, 3) метод оптимизации. 1) последоват пороговый – выбирают кластер и все об., наход в пределах заданного от центра порогового знач, группируют вместе. Далее выбир-ся нов центр и процесс повтор-ся для не вошедших в кластеры объектов и т.д. 2) параллельный пороговый - одновременно опр-ют несколько класт центров. После форм-ния кластеров пороговое знач мб скорректир., что позволяет отрегул кол-во наблюдений в кластере. 3) метод оптимизации позволяет поставить объекты в соотв другим кластерам, чтобы оптимизир суммарный критерий. 3 этап. Выбор меры расстояния. Чтобы сгруппировать наблюдения в кластеры, необх рассчитать какой-л пок-ль сходства или различия между объектами: 1) евклидово расстояние; 2) квадрат евклид расстояния; 3) корреляция Пирсона; 4) мера хи-квадрат и др. 4 этап. Опр-ние кол-ва кластеров. Оптим явл-ся такое кол-во кластеров, при кот сформир кластеры: 1) объедин в себе как можно больше объектов исслед., 2) являются возможно менее гетерогенными внутри (разнород.). Оптим кол-во кластеров опр-ся специалистами. Подходы: 1) опр-ние, основ на предвар инф-ции, т.е. опыте и знаниях, 2) на основании модели кластеров, 3) на основе завис-ти дисперсии от числа кластеров, 4) опр-ние на основе размеров кластеров. 5 этап. Интерпретация, профилирование кластеров. После формир-я кластеров их нужно описать. Центроид – ср знач объектов кластера по каждой из перем., формир-х профиль каждого об. Если сущ-ют знач различия между перем в кластерах, целесообр исп-ть дисперс/ дискр анализ. 6 этап. Оценка достоверности кластеризации. 1) исп-ние разных способов измер расстояния для сравнения рез-тов, 2) исп-ние разл методов КА для сравнения рез-тов, 3) выполнение КА для 2 подвыборок, 4) выполнение КА по сокращ набору перем., т.е. случ удаление неск перем для сравнения с полным набором перем., 5) изменение порядка случаев при иерарх подходе до получения стабильного решения.
|

 2) значения остаточного ряда должны быть случайны. Критерий пиков (поворотных точек). Точка считается поворотной, если она либо больше и предыдущего и последующего значения, либо меньше. В случайном ряду должно выполнятся строгое неравенство
2) значения остаточного ряда должны быть случайны. Критерий пиков (поворотных точек). Точка считается поворотной, если она либо больше и предыдущего и последующего значения, либо меньше. В случайном ряду должно выполнятся строгое неравенство 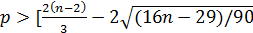 , где p – число поворотных точек. 3) Независимость значений ej, что определяется отсутствием в остаточном ряду автокорреляции под которой понимается корреляция между элементами одного и того же числового ряда. 4) Наличие автокорреляции может быть выявлено при помощи d-критерия Дарбина-Уотсона.
, где p – число поворотных точек. 3) Независимость значений ej, что определяется отсутствием в остаточном ряду автокорреляции под которой понимается корреляция между элементами одного и того же числового ряда. 4) Наличие автокорреляции может быть выявлено при помощи d-критерия Дарбина-Уотсона.  . Расчетное значение критерия сравнивают с табличными значениями. Если d принадлежит (d2;2) – автокорреляция отсутствует; 4) Соответствие остаточного ряда нормированному распределению. Для проверки используется RS-критерий
. Расчетное значение критерия сравнивают с табличными значениями. Если d принадлежит (d2;2) – автокорреляция отсутствует; 4) Соответствие остаточного ряда нормированному распределению. Для проверки используется RS-критерий  , где emax emin – максимальное и минимальное значение ряда остатков, S- среднеквадратичное отклонение значений остаточного ряда. Если рассчитанное значение попадает между границами с заданным уровнем вероятности, то гипотеза о нормированном распределении принимается.
, где emax emin – максимальное и минимальное значение ряда остатков, S- среднеквадратичное отклонение значений остаточного ряда. Если рассчитанное значение попадает между границами с заданным уровнем вероятности, то гипотеза о нормированном распределении принимается.


