Корреляционный анализ.
Корреляционный анализ - стат. метод, позволяющий измерить силу связи между двумя или более переменными и рассматривающий совместно изменение 2- х оцениваемых переменных. Корреляционный анализ применяют в случаях, когда исследователя интересуют связь между 2 метрическими переменными. Например: * насколько сильно связан V продаж с расходами на сервисное обслуживание? * существует ли связь между долей рынка и расходами га рекламу? Статистики, используемые в корреляц. анализе: Коэффициент парной корреляции r (коэф. коррел. Пирсона, линейный коэф. корреляции) - стат. показатель, характеризующий степень тесноты между 2 метрическими переменными. Данный показатель показывает меру зависимости между переменными Х и Y, при этом его использ. в случае линейной зависимости между переменными. Если между переменными нет лин. зависимости, коэф: корреляции будет =0, при этом это не значит, что связи между переменными нет. Коэф. парной корреляции r, для переменных Х и Y:
где n- размер выборки;
Ковариация - систематич. взаимосвязь между 2 переменными, при которой изменение 1 переменной вызывает соотв. изменение другой переменной. Ковариация м/б как положительной, так и отрицательной. Коэф. корреляции r €[0:1]. Чем ближе знач. к 1, тем сильнее связь. Статистическая значимость (измер. коэф. корреляции) ρ- коэф. корреляции, кот. вычисляется для всей генеральной сов-ти: Гипотезы имеют вид: Ho: ρ =0 H1: ρ ≠0 Для проверки гипотезы исп. t- статистику.
где n-2 -число степеней свободы. Корреляц. матрица показывает коэф. корреляции между каждой парой данных. Частный коэф. корреляции - мера зависимости между 2 переменными после фикссации (исключение, корректировки) эффектов 1 или неск. переменных. Например: зависит ли V продаж от расходов на реклааму, если исключить эффект влияния цены? Он вычисляется исходя из значений простых коэф. корреляции:
где Частичный коэф. корреляции - мера зависимости между Y и X, когда линейные эффекты др. независимых переменных исключены из X (но не из Y).
Показатели неметрической корреляции: * коэф-ты ранговой корреляции Спирмена Коэф-нт ранговой корреляции находится в пределах от -1 до +1, при этом:
0,4≤ Коэф-нт ранговой корреляции Спирмена целесообразно использовать в случае большого числа категорий, что приводит к небольшому кол-ву совпадающих рангов. * Коэф-нт ранговой корреляции Кендалла целесообразно использовать, когда большинство наблюдений попадает в относительно небольшое число категорий, что приводит к большому кол-ву связанных рангов.
|

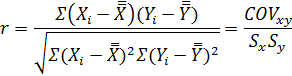
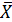 ,
,  - выбарочное средние;
- выбарочное средние;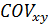 - ковариация между Х и Y;
- ковариация между Х и Y; и
и  - стандартные отклонения.
- стандартные отклонения.

 ,
,  - коэффициенты парной корреляции между X и Z, Y и Z.
- коэффициенты парной корреляции между X и Z, Y и Z.
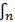 ≤0,3 показатель слабой тесноты связи;
≤0,3 показатель слабой тесноты связи;


