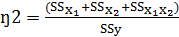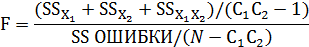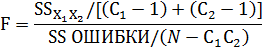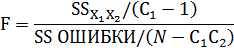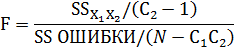Многофакторный дисперсионный анализ. Ковариационный анализ.
Многофакторный дисперсионный анализ - модель дисперсионного анализа, которая включает 2 и более факторов и позволяет изучить их взаимодействие. Межфакторное взаимодействие между переменными имеет место тогда, когда влияние 1 фактора зависит от уровня др. факторов. 1 этап: Определение зависимой и независимой переменной. Зависимая переменная (Y) - метрическая переменная Независимые переменные (Х1 и Х2)- категориальные переменные (факторы), имеющие соответственно С1 и С2 категорий (групп, уровней). 2 этап: Разложение полной вариации SSy=SSХ1+SSX2+SSX1X2+SS ОШИБКИ SSy- полная дисперсия перем. Y SSX1X2 - вариация переменной Y, связ. с взаимодействием Х1 и Х2. Значение SSX1X2 зависит от силы взаимодействия факторов Х1 и Х2 между собой: если Х1 и Х2 не зависят один от другого, значения SSX1X2 приближается к нулю. 3 этап: Измерение эффекта. Степень объединенного влияния 2- х (или более) факторов называют полным эффектом или множественной корреляцией ŋ2: 4 этап: Проверка значимости. Значимость полного эффекта - проверка наличия различий между некоторыми из групп факторного эксперимента. Значимость полного эффекта проверяется с помощью F- критерия:
5 этап: изучение значимости эффекта взаимодействия. Если полный эффект стат. значимый, то на след. этапе изучают значимость эффекта взаимодействия. Для этого производят расчёт F- критерия:
Если эффект взаимодействия стат. значимый, то эффект Х1 зависит от Х2 и наоборот. Если эффект взаимодействия стат. незначим, осуществляется проверка значимости главного эффекта каждого фактора:
|