Показатели оценки статистической значимости и тесноты связи переменных, включенных в состав таблицы сопряженности.Стат критерий χ2 исп. для проверки стат значимости наблюдаемых связей в таблицах сопряженности признаков и позволяет определить наличие или отсутствие значимой связи между 2 переменными. Коэф. Фишера исп. для измерения тесноты связи при анализе таблиц с 2 строками и 2 столбцами: Ф = Коэф. «лямбда» исп. в случае измерения переменных с пом. номин. шкалы. Ассимметр. коэф. «лямбда» - мера выраженного в % улучшения прогнозирования значения зависимой переменной при данном значении независимой. Если =1, то прогноз мб сделан без ошибок. Рассчитывается для каждой из зависимых. Симметричный – мера выраженного в % общего улучшения прогнозирования, когда прогноз сделан в обоих направлениях.
37. Проверка гипотез о различиях между значениями переменных: параметрические методы. Параметрические методы применяются в случае, если данные представлены интервальной шкалой. В случае если исследуется 1 выборка, для определения различий между значениями переменных используется t-критерий и z-критерий. При исследовании 2-х независимых выборок используется двухгрупповой t-критерий или F-критерий для среднего и z-критерий для доли. При исследовании 2-х парных выборок используется парный t-критерий.
38. Проверка гипотез о различиях между значениями переменных: непараметрические методы. Непараметрические методы применяются в случае, если данные представлены номинальной или порядковой шкалой. В случае если исследуется 1 выборка, для определения различий между значениями переменных используется критерий χ2 и критерий Колмогорова-Смирнова. При исследовании 2-х независимых выборок используется критерий χ2 двухвыборочный критерий Колмогорова-Смирнова, медианный U-критерий. При исследовании 2-х парных выборок используется критерий χ2 критерий знаков, критерий Вилкоксона.
39. Однофакторный дисперсионный анализ (ОДА). ДА – статистический метод изучения различий между выборочными средними для 2 и более совокупностей. Процедура выполнения ОДА: 1) определение зависимой и независимой переменной; Для каждой группы наблюдений Х существует n наблюдений Y, соответственно размер выборки в каждой группе X=n. Размер общей выборки: N=n*c, где n – кол-во наблюдений; с – кол-во категорий. Обязательные условия: · зависимая переменная д.б. измерена с помощью интервальной или относительной шкалы; · наличие категориальной независимой переменной (1 или больше), называемой фактором. Однофакторная дисперсионная модель: Xij = μ+Fi+εij, где Xij – значение исследуемой переменной, полученное на i-ом уровне фактора с j-ым №. μ – общая средняя. Fi – эффект, обусловленный влиянием i-ым уровнем фактора. εij – остаточный член, значения которого определяются влиянием неконтролируемых факторов. 2) разложение полной дисперсии – разделение дисперсии зависимой переменной на дисперсию, обусловленную внутригрупповой изменчивостью: SSY = SSмежгрупповая+SSвнутригрупповая = SSх+SSошибки SSY – полная дисперсия переменной Y. SSмежгрупповая – вариация переменных Y, обусловленная различием средних между группами. SSвнутригрупповая – вариация переменных Y, обусловленная вариацией внитри каждой группы категорий. SSY = Yi – отдельное наблюдение; Yij – i-ое наблюдение в j-ой группе;
|
где fe = 
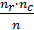foij – наблюдаемое, feij – ожидаемое кол-во случаев в (ij)-й клетке, nr – итоговое число в строке, nc – в колонке, n – полный размер выборки, r – кол-во строк, с – столбцов. Найденное расчетное χ2 сравнивается с таблицей критич. значений для опред. числа степеней свободы: (r-1) (c-1). Если расчетное значение χ2 > χ кр, то Н0 отклоняется.
где n – размер выборки. Если Ф =0, то связь отсутствует, а при сильной связи Ф →1 (Ф>;0,5 – связь сильная). Коэф. сопряженности признаков Пирсона – мера тесноты связи для таблиц любого размера. С = 
Чем ближе к 1, тем теснее связь. V-коэф. Крамера – мера тесноты связи, исп. в таблицах больших по размеру, чем 2х2. V =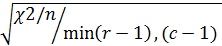 
или V= 
Чем ближе к 1, тем теснее связь.
; SSмежгрупповая = 
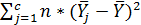; SSошибки = 
, где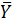
- средняя для всей выборки; 
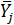- средняя для j-ой группы.
