Множественный регрессионный анализ. Нелинейная регрессия.
Множественная регрессия – статистический метод, с помощью которого можно вывести математическую зависимость между двумя или более независимыми и зависимой переменной, выраженной с помощью интервальной или относительной шкалы. Этапы: 1) Формулирование модели. Общая форма имеет вид 2)Вычисление параметров. Модель множественной регрессии оценивается следующим уравнением: 3) Вычисление нормированного коэффициента регрессии (бета коэффициента) – частотного коэффициента регрессии рассчитанного при условии, что все данный нормированы. 4) Определение тесноты и значимости связи. Разложение полной вариации SSy=SSрегр+SSошибки. Тесноту связи при множественной регрессии измеряют при помощи коэфициента множественной детерминации R2. R2=SSрегрессии/SSy. Данный коэффициент корректируют с учетом числа независимых переменных (k) и размера выборки (n), чтобы снизить влияние зависимость коэфициента детерминации от количества переменных. Скор. R2= 5) Проверка значимости включает проверку значимости общего уравнения регрессии и частных коэффициентов регрессии. Н0: коэффициент множественной детерминации для генеральной совокупности R2=0, R2совокупности= 0 Общую проверку выполняют с помощью F-статистики. 6) Анализ остатков. Остаток – разность между наблюдаемым значением Y и его теоретическим значением, предсказанным уравнением регрессии. Анализ производится для подтверждения того, что модель регрессии подходит для анализа, с этой целью используется графический метод. Сумма квадратов остатков измеряет необъясненную часть вариации зависимой переменной. RSS=∑ei2. Используется как основная минимизирующая велечина в методе наименьших квадратов.
|

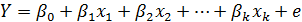
 , где Y-вычисляемое значение Yi; a- отрезок отсекаемый на оси Oy, bi - частные коэффициенты регрессии. bi – обозначает изменение в значении Y, при изменении Х1 на единицу, когда другие независимые Х остаются неизменными. Поэтому b-коэффициент парной регрессии для Y от Х1, при исключении эффекта переменных от Х2 до Хk. Результаты совместного влияния х1, х2 … на y суммируются, т.е. ожидаемое изменение значения Y будет равно ∑bi
, где Y-вычисляемое значение Yi; a- отрезок отсекаемый на оси Oy, bi - частные коэффициенты регрессии. bi – обозначает изменение в значении Y, при изменении Х1 на единицу, когда другие независимые Х остаются неизменными. Поэтому b-коэффициент парной регрессии для Y от Х1, при исключении эффекта переменных от Х2 до Хk. Результаты совместного влияния х1, х2 … на y суммируются, т.е. ожидаемое изменение значения Y будет равно ∑bi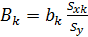

 , где n-k-1 – число степеней свободы. Если Н0 отклоняют, то выполняют дополнительную проверку, чтобы определить какие Bi отличны от 0, используя t-статистику. t(b)= b/SE(b), SE – стандартная ошибка коэффициента регрессии
, где n-k-1 – число степеней свободы. Если Н0 отклоняют, то выполняют дополнительную проверку, чтобы определить какие Bi отличны от 0, используя t-статистику. t(b)= b/SE(b), SE – стандартная ошибка коэффициента регрессии


