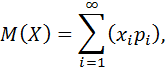Оценка.

№ 1. Исходные данные. Доход индивида составляет 180 ден. ед. в месяц. Функция полезности имеет вид: U (X, Y) = X ´ Y ².

1. Проанализируйте, в том числе графически, эффект Веблена, эффект сноба и эффект подражания большинству. Приведите примеры описываемых эффектов. (5 баллов)

2. Определите аналитически функцию спроса индивида на товар Х и функцию спроса индивида на товар Y. Покажите эти функции на графике. (5 баллов)

3. Опередите расходы индивида на товар Y, если цена товара Y равна 5 ден. ед. за штуку. Как изменятся расходы индивида на данный товар, если цена товара Y возрастет в два раза; доход увеличится до 270 ден. ед. Покажите на графике, как будут выглядеть последствия указанных изменений. (5 баллов)

4. Рассчитайте коэффициенты прямой и перекрестной эластичности спроса по цене на товар Y, при цене товара Y равной 5 ден. ед. за штуку и первоначальном уровне дохода. Прокомментируйте полученные результаты. (5 баллов)

№ 2. Исходные данные. Монополия с функцией общих затрат TC = 50 + 2 Q ² максимизирует прибыль при отраслевом спросе Q^D = 180 – 2 P.

1. Определите понятие «ценовая дискриминация 3-ей степени», объясните ее сходство и различие с ценовой дискриминацией 2-ой степени и назовите условия ее осуществления. Приведите примеры ценовой дискриминации 3-ой степени из практики. (5 баллов)

2. Докажите аналитически и покажите графически, что при переходе от единой цены на всех сегментах монополизированного рынка к ценовой дискриминации 3-й степени сумма излишков производителей и потребителей может, как увеличится, так и уменьшится. (5 баллов)

3. Определите цену, объем производства, прибыль монополии и излишки потребителей. Решение представьте графически. (5 баллов)

4. Сравните, как измениться цена и сумма прибыли по пункту 2, со случаем когда монополия будет уплачивать налог на капитал в размере 100 ден. ед. Приведите не менее двух примеров налога на капитал, из реальной экономической практики. Решение представьте графически. (5 баллов)

5. Определите объем продаж, цену и выручку монополии, если по сравнению с исходными условиями рыночный спрос возрастет так, что при каждой цене объем спроса увеличится на 36 ед. (5 баллов)

6. Сравните, насколько изменится сумма прибыли монополии и излишки потребителей, если монополия будет осуществлять совершенную ценовую дискриминацию. Решение представьте графически. (5 баллов)

 

Биржевые стратегии, составление портфеля инвестиций и диверсификация средств в различные бумаги основываются на весьма относительно прогнозируемых значениях. В этом смысле рынок представляет собой место концентрации неограниченного количества факторов, которые и определяют цену бумаги. Как следствие неизвестная природа фактов не позволяет точно предсказать дальнейшее развитие событий на бирже.

Именно поэтому сведение вероятности того, что цена все же достигнет запланированной отметки в 100, 200 или 300 пунктов, к математическим параметрам является фактором, отличающим, способ мышления профессионала от неудачника.

Под словом ожидание следует подразумевать «математическое ожидание случайной величины» - [M (X)], т.е. конкретное число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание равно среднему арифметическому бесконечного количества значений случайной величины:

где x_i – значение, а p_i вероятность.

Несовпадение конечных значений с нашими ожиданиями – это отклонение от ожидания. Отклонением называют разность между случайной величиной и её математическим ожиданием, где X – случайная величина и M(X) – её математическое ожидание:

X – M (X).

Однако, на практике как таковое отклонение случайной величины от её математического ожидания не применяется, т.к. математическое ожидание отклонения равно нулю:

M [ X – M (X) ] = 0.

Другими словами, математическое ожидание не предполагает и не может предполагать отклонение от самого себя. Эти соображения говорят о целесообразности заменить возможные отклонения их абсолютными значениями или их квадратами.

Оценка.

Приведенное выше теоретическое описание математического ожидания играет большую роль для понимания следующих обоснований. Однако, в дальнейшем мы будем пользоваться понятием «оценка», а не классическое «мат ожидание».

Оценка [μ]- это число, вычисляемое на основе наблюдений, которое предположительно близко к оцениваемому параметру. Она описывается следующей формулой:

μ =

где x_i – значение, N – размер выборки (количество значений).

Различие между оценкой и мат ожиданием заключается в том, что первое характеризуется теоретическим расчетом значений на основе знаний о процессе. Математическое ожидание же напротив, оперирует расчетом на основе бесконечной выборки.

В случае, когда возможные отклонения заменяют их абсолютными значениями, приходится оперировать с абсолютными величинами, что приводит к серьезным затруднениям. Поэтому чаще всего вычисляют среднее значение квадрата отклонения, которое и называют дисперсией.