Показатели состояния технологического процесса
Статистический анализ заключается в выявлении закона распределения производственных погрешностей при производстве продукции, нахождении оценок его параметров и вычислении необходимых показателей, характеризующих состояние технологического процесса. Для установления закона распределения контролируемого параметра необходимо отобрать не менее 100 единиц продукции (по ряду мгновенных выборок при неизменной настройке технологического процесса) и измерить значения контролируемого параметра. Далее следует выбрать подходящую систему непрерывных распределений и по соответствующей программе найти выравнивающее распределение и оценки его параметров. Найденный закон распределения случайной величины является наиболее полной ее характеристикой. Более того, он позволяет рассчитывать показатели состояния технологического процесса (при условии его статистической управляемости, когда устранены грубые отклонения от нормы). Одним из таких показателей является показатель точности процесса (коэффициент рассеяния). Он вычисляется по формуле [6, c.32; 19, c.6; 20]
где Ширина поля рассеяния вычисляется при условии, что 99,73% значений контролируемого параметра находятся внутри границ поля рассеяния. Для нормального закона ω = 6 S, где S – выборочное среднее квадратическое отклонение. При использовании обобщенных распределений ширину поля рассеяния будем определять из того же условия, т.е. Р=F(xВ)-F(xН)= 0,9973, при этом значения функции распределения F(ХН)= 0,00135, F(ХВ)= 1–0,00135=0,99865. Чем меньше ширина поля рассеяния, тем точнее технологический процесс. Однако один показатель меры точности – коэффициент К т – не в полной мере характеризует технологический процесс. В случае, когда центр статистического распределения Систематические погрешности характеризуются коэффициентом смещения (точности настройки), или показателем уровня настройки [19, c.6]
где В заключение статанализа вычисляется предполагаемый уровень брака q, выраженный в процентах. Он находится по формуле (см. рис. 9.1.1)
При этом брак на нижней границе поля допуска равен
а на верхней границе
Рис. 9.1.1. Показатели состояния технологического процесса
Отметим, что при условии, когда показатель уровня настройки КН= 0 (при этом Е = 0), а показатель точности КТ = 1, предполагаемый процент брака q=qн+qв не превышает 0,27%. С ростом КТ он увеличивается. В большинстве случаев достаточно обеспечить КТ ≤ 0,75. Для ответственных технологических процессов необходимо иметь КТ = 0,4 Закон распределения контролируемого показателя качества наиболее полно характеризует технологический процесс. Если за некоторое время закон распределения не изменился, т.е. не изменились его параметры, например, центр распределения и среднее квадратическое отклонение, или изменились в допустимых пределах, то процесс считается стабильным. Изменение значений центра распределения и среднего квадратического отклонения за допустимые пределы требует переналадки процесса, так как он утратил стабильность. Нестабильность технологического процесса по уровню настройки принято характеризовать коэффициентом смещения настройки [4, c.96]
где Нестабильность технологического процесса по рассеянию характеризуют коэффициентом межнастроечной стабильности [4, c.97]
где Поскольку статистические распределения часто имеют асимметрию, то показатель уровня настройки целесообразно вычислять не по формуле (9.1.2), в которую входит центр распределения
где
Т0 , Х0 – середины полей допуска и рассеяния; они вычисляются по формулам
С учетом (9.1.10) формула (9.1.8) может быть представлена в виде
Рассмотрим случай, когда коэффициент точности КТ ≤ 1. Пусть ТН = ХН, т.е. нижние границы конструкторского и технологического допусков совпадают. При этом условии на нижней границе конструкторского допуска брак не будет превышать допустимого значения. Формула (9.1.11) примет вид
Но ТН = ХН, следовательно,
Пусть далее ТВ = ХВ. В этом случае на основании (9.1.11) имеем
Заменяя ХВ на ТВ , получим
Следовательно, условие, при котором брак не превышает допустимого уровня, задается неравенством
или
Для регулирования ТП необходимо установить исправленное среднее значение контролируемого параметра, которое вычисляется по формуле
Последняя формула следует из равенства Т0=Х0+а (см. формулу 9.1.9). При КТ > 1 необходимо принять все меры для уменьшения поля рассеяния контролируемого параметра. Установим связь между объемом выборки n и показателями КТ, КН. Для того чтобы гарантировать выпуск бездефектной продукции, необходимо, чтобы поле конструкторского допуска было шире поля рассеяния как минимум на величину Итак, пусть
Тогда коэффициент точности в общем случае будет задаваться формулой
В частном случае, если случайная величина Х распределена по нормальному закону, из (9.1.15) имеем
Тогда коэффициент уровня настройки на основании (9.1.12) и (9.1.16) будет равен
При n = 100 имеем: При n = 25 При n = 9 При этих значения КТ и КН брак не превышает предельного уровня. Из формулы (9.1.14) можно найти требуемое значение среднего квадратического отклонения (в случае нормального закона)
а также требуемое значение допуска при заданном σ х
9.2. Пример статистической обработки результатов замера контролируемого параметра по программе Были измерены отклонения от номинального размера некоторой детали Ø50 мм. Конструкторский допуск равен ±0,012 мм, т.е. ТН =–0,012, ТВ =+0,012. Ширина поля допуска ТХ=ТВ–ТН= 0,024 мм. Результаты замеров (в микронах) представлены в контрольном листке. Точность измерительного средства равна 0,002 мм и составляет 1/12 ширины конструкторского допуска. Объем выборки n = 100. Найдем выравнивающую кривую распределения по несгруппированным данным. Запустив Программу, введем по одному значению табличные данные, нажимая каждый раз клавишу ‹ENTER› (ВВОД). При этом вместо значения 0 будем вводить 0,000001. Для завершения введем 0. Получим множество показателей статистического распределения. Статистические данные контрольного листка можно представить в более компактном виде, если объединить одинаковые значения отклонений от номинального размера (табл. 9.2.2).
Таблица 9.2.1
|

 , (9.1.1)
, (9.1.1) - ширина поля рассеяния (технологический допуск); ХВ, ХН – верхняя и нижняя границы поля рассеяния; δ = ТВ – ТН - ширина поля допуска (конструкторский допуск); ТВ , ТН – верхняя и нижняя границы поля допуска. В зарубежной литературе используется индекс Ср = 1 /КТ.
- ширина поля рассеяния (технологический допуск); ХВ, ХН – верхняя и нижняя границы поля рассеяния; δ = ТВ – ТН - ширина поля допуска (конструкторский допуск); ТВ , ТН – верхняя и нижняя границы поля допуска. В зарубежной литературе используется индекс Ср = 1 /КТ. смещен относительно середины поля допуска Т0, т.е. имеются систематические погрешности, процесс может не обеспечивать изготовление бездефектной продукции.
смещен относительно середины поля допуска Т0, т.е. имеются систематические погрешности, процесс может не обеспечивать изготовление бездефектной продукции. , (9.1.2)
, (9.1.2)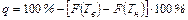 . (9.1.3)
. (9.1.3) , (9.1.4)
, (9.1.4) . (9.1.5)
. (9.1.5)
 [6, c.32].
[6, c.32]. , (9.1.6)
, (9.1.6) - начальное и конечное (на момент времени t) значения центра распределения.
- начальное и конечное (на момент времени t) значения центра распределения. , (9.1.7)
, (9.1.7) - начальное и конечное (на момент времени t) значения среднего квадратического отклонения.
- начальное и конечное (на момент времени t) значения среднего квадратического отклонения. , (9.1.8)
, (9.1.8) , (9.1.9)
, (9.1.9) . (9.1.10)
. (9.1.10) . (9.1.11)
. (9.1.11) .
. .
. .
. .
. ,
, . (9.1.12)
. (9.1.12) . (9.1.13)
. (9.1.13) , где
, где  – среднее квадратическое отклонение среднего арифметического.
– среднее квадратическое отклонение среднего арифметического. . (9.1.14)
. (9.1.14) . (9.1.15)
. (9.1.15) . (9.1.16)
. (9.1.16) . (9.1.17)
. (9.1.17) .
. .
.
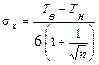 , (9.1.18)
, (9.1.18) . (9.1.19)
. (9.1.19)



