Метод обобщения
Рассмотрим уравнения экспоненты и прямой:
Найдем такую обобщенную формулу, которая будет включать множество частных случаев, в том числе уравнения прямой и экспоненты. Обобщим две последние формулы путем введения нового параметра u. Используя замечательный предел
представим обобщенное уравнение в виде
При u = 1 из (11.2.1) имеем прямую, при u →0 – экспоненту. Если из опыта величина y0 неизвестна, то формулу (11.2.1) целесообразно представить в другом виде
Чтобы увеличить аппроксимирующие возможности формул (11.2.1) и (11.2.2), введем в них дополнительный параметр β
Исследуем темп прироста кривой (11.2.3). Для этого вначале прологарифмируем ее:
Тогда
В частном случае, при u →0
Из последней формулы следует, что при β = 1 (u →0) мгновенный темп прироста (и, следовательно, темп роста) не зависит от времени t. При β>1 темп прироста со временем растет, при β<1 – убывает. Это значит, что параметр β является показателем ускорения или замедления темпа прироста (и темпа роста) кривой (11.2.3), которая при u →0 имеет вид
Из (11.2.5) следует, что при β = 1, u < 0 темп прироста кривой (11.2.3) со временем растет, а при u > 0 – убывает. По характеру темпа прироста эмпирического временного ряда может быть установлена выравнивающая кривая, обладающая нужными свойствами. На основании формул (11.2.3) и (11.2.4) можно получить другие кривые роста. Например, при t = ex
При
Приведенные четырехпараметрические кривые роста содержат множество частных случаев и могут использоваться в различных областях знания для выравнивания и прогнозирования различных статистических зависимостей, в том числе временных рядов.
|

 .
. ,
, (11.2.1)
(11.2.1)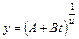 , (11.2.2) где
, (11.2.2) где  .
. (11.2.3)
(11.2.3) . (11.2.4)
. (11.2.4) .
. . (11.2.5)
. (11.2.5)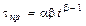 . (11.2.6)
. (11.2.6) . (11.2.7)
. (11.2.7) , (11.2.8)
, (11.2.8)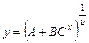 . (11.2.9)
. (11.2.9)
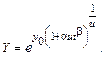 (11.2.10)
(11.2.10) . (11.2.11)
. (11.2.11)


